Question

（2011•东城区二模）已知点P（2，t）在不等式组

x-y-4≤0 x+y-3≤0

表示的平面区域内，则点P（2，t）到直线3x+4y+10=0距离的最大值为

4

．

Answer 1

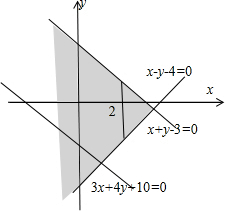
分析：画出不等式组表示的可行域，结合P的坐标，求出t的范围，利用点到直线的距离公式，通过t的范围求出距离的最大值．

解答：解：由P（2，t）在不等式组

x-y-4≤0 x+y-3≤0

表示的平面区域内，当x=2时，2-t-4≤0，解得t≥-2，
2+t-3≤0，解得t≤1，可得t∈[-2，1]，
点P（2，t）到直线3x+4y+10=0距离d=

|16+4t|

5

，
当t=1时距离最大d=

|16+4×1|

5

⇒dmax=4．

故答案为：4．

点评：本题是中档题，考查点到直线的距离公式的应用，线性规划的应用，考查数形结合，计算能力，转化思想．