题目内容
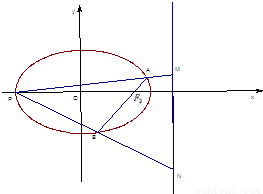
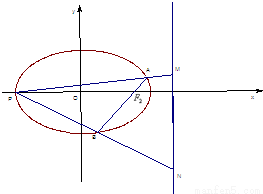
如图,已知A是椭圆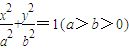 上的一个动点,F1,F2分别为椭圆的左、右焦点,弦AB过点F2,当AB⊥x轴时,恰好有|AF1|=3|AF2|.
上的一个动点,F1,F2分别为椭圆的左、右焦点,弦AB过点F2,当AB⊥x轴时,恰好有|AF1|=3|AF2|.(1)求椭圆的离心率;
(2)设P是椭圆的左顶点,PA,PB分别与椭圆右准线交与M,N两点,求证:以MN为直径的圆D一定经过一定点,并求出定点坐标.
【答案】分析:(1)由已知中AB⊥x轴时恰有|AF1|=3|AF2|.结合椭圆的定义,可得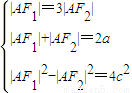 ,进而求出椭圆的离心率;
,进而求出椭圆的离心率;
(2)由(1)可设椭圆方程为x2+2y2=2b2,其右准线方程为x=2b,分AB⊥x轴时和AB斜率存在时两种情况分别判断F2与MN为直径的圆D的关系,即可得到答案.
解答:解:(1)由条件可得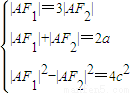 ,
,
解得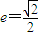 ….(3分)
….(3分)
证明:(2)由(1)可设椭圆方程为x2+2y2=2b2,其右准线方程为x=2b,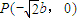
①当AB⊥x轴时,易得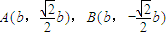 ,
,
由三点共线可得M(2b,b),N(2b,-b)
则圆D的方程为(x-2b)(x-2b)+(y-b)(y+b)=0,
即(x-2b)2+y2=b2
易得圆过定点F2(b,0)…(6分)
②当AB斜率存在时,设其方程为y=kx-kb,M(x1,y1),N(x2,y2),
把直线方程代入椭圆方程得:(1+2k2)x2-4k2bx+(2k2-2)b2=0∴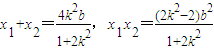
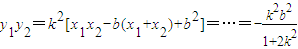 ,
,
故直线AP的方程为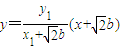 ,
,
令x=2b得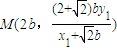 ,同理可得
,同理可得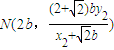 …(9分)
…(9分)
∴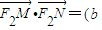 ,
,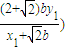 •
•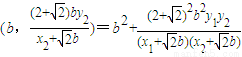 =
=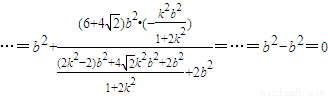
所以F2在以MN为直径的圆D上,
综上,以MN为直径的圆D一定经过定点F2(b,0)….(13分)
点评:本题考查的知识点是直线与圆锥曲线的综合应用,椭圆的性质,圆的标准方程,综合性强,难度较大.
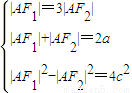 ,进而求出椭圆的离心率;
,进而求出椭圆的离心率;(2)由(1)可设椭圆方程为x2+2y2=2b2,其右准线方程为x=2b,分AB⊥x轴时和AB斜率存在时两种情况分别判断F2与MN为直径的圆D的关系,即可得到答案.
解答:解:(1)由条件可得
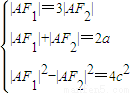 ,
,解得
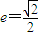 ….(3分)
….(3分)证明:(2)由(1)可设椭圆方程为x2+2y2=2b2,其右准线方程为x=2b,
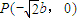
①当AB⊥x轴时,易得
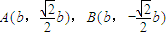 ,
,由三点共线可得M(2b,b),N(2b,-b)
则圆D的方程为(x-2b)(x-2b)+(y-b)(y+b)=0,
即(x-2b)2+y2=b2
易得圆过定点F2(b,0)…(6分)
②当AB斜率存在时,设其方程为y=kx-kb,M(x1,y1),N(x2,y2),
把直线方程代入椭圆方程得:(1+2k2)x2-4k2bx+(2k2-2)b2=0∴
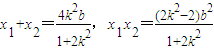
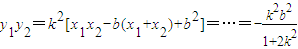 ,
,故直线AP的方程为
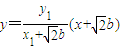 ,
,令x=2b得
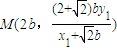 ,同理可得
,同理可得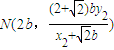 …(9分)
…(9分)∴
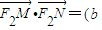 ,
,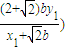 •
•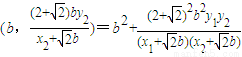 =
=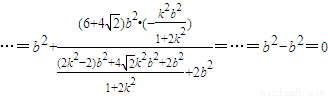
所以F2在以MN为直径的圆D上,
综上,以MN为直径的圆D一定经过定点F2(b,0)….(13分)
点评:本题考查的知识点是直线与圆锥曲线的综合应用,椭圆的性质,圆的标准方程,综合性强,难度较大.

练习册系列答案
相关题目
 (2011•江西模拟)如图,已知A是椭圆
(2011•江西模拟)如图,已知A是椭圆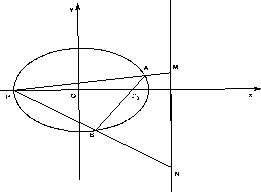
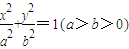 上的一个动点,F1,F2分别为椭圆的左、右焦点,弦AB过点F2,当AB⊥x轴时,恰好有|AF1|=3|AF2|.
上的一个动点,F1,F2分别为椭圆的左、右焦点,弦AB过点F2,当AB⊥x轴时,恰好有|AF1|=3|AF2|.