题目内容
定义在R上的偶函数y=f(x)在(-∞,0]上递增,函数f(x)的一个零点为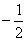 ,求满足
,求满足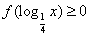 的x的取值集合.
的x的取值集合.
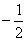 ,求满足
,求满足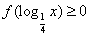 的x的取值集合.
的x的取值集合. 解:∵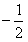 是函数的零点,∴f(
是函数的零点,∴f( )=0,
)=0,
∵f(x)为偶函数,∴f( )=0,
)=0,
∵f(x)在(-∞,0]上递增,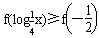 ,
,
∴0≥ ≥
≥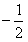 ,∴1≤x≤2,
,∴1≤x≤2,
∵f(x)为偶函数,
∴f(x)在[0,+∞)上单调减,
又f(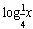 )≥f(
)≥f(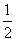 ),
),
∴0≤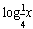 ≤
≤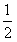 ,
,
∴ ≤x≤1,∴
≤x≤1,∴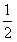 ≤x≤2,
≤x≤2,
故x的取值集合为{x|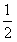 ≤x≤2}.
≤x≤2}.
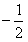 是函数的零点,∴f(
是函数的零点,∴f( )=0,
)=0,∵f(x)为偶函数,∴f(
 )=0,
)=0,∵f(x)在(-∞,0]上递增,
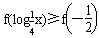 ,
,∴0≥
 ≥
≥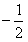 ,∴1≤x≤2,
,∴1≤x≤2,∵f(x)为偶函数,
∴f(x)在[0,+∞)上单调减,
又f(
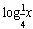 )≥f(
)≥f(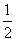 ),
),∴0≤
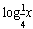 ≤
≤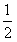 ,
,∴
 ≤x≤1,∴
≤x≤1,∴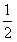 ≤x≤2,
≤x≤2,故x的取值集合为{x|
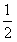 ≤x≤2}.
≤x≤2}. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目