题目内容
定义在R上的偶函数y=f(x)满足:①对x∈R都有f(x+6)=f(x)+f(3);②当x1,x2∈[0,3]且x1≠x2时,都有
>0,若方程f(x)=0在区间[a,8-a]上恰有3个不同实根,实数a的取值范围是
| f(x1)-f(x2) | x1-x2 |
(-7,-3)
(-7,-3)
.分析:利用条件确定函数的周期性,利用周期性,奇偶性和单调性之间的关系,利用数形结合确定方程区间的取值范围.
解答:解:∵f(x+6)=f(x)+f(3),
∴当x=-3时,f(-3+6)=f(-3)+f(3),
即f(3)=2f(3),∴f(3)=0,
即f(x+6)=f(x)+f(3)=f(x),
∴函数的周期是6.
∵当x1,x2∈[0,3]且x1≠x2时,都有
>0,
∴函数f(x)在[0,3]上单调递增,
∵数y=f(x)是偶函数,∴函数f(x)在[-3,0]上单调递减.
∵区间[a,8-a]关于x=
=4对称.
则由8-a-a>0,解得a<4.
∵-3关于x=4对称的点为x=11,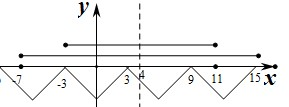
15关于x=4对称的点为x=-7,
∴要使方程f(x)=0在区间[a,8-a]上恰有3个不同实根,
则11<8-a<15,
解得-7<a<-3,
故答案为:(-7,-3).
∴当x=-3时,f(-3+6)=f(-3)+f(3),
即f(3)=2f(3),∴f(3)=0,
即f(x+6)=f(x)+f(3)=f(x),
∴函数的周期是6.
∵当x1,x2∈[0,3]且x1≠x2时,都有
| f(x1)-f(x2) |
| x1-x2 |
∴函数f(x)在[0,3]上单调递增,
∵数y=f(x)是偶函数,∴函数f(x)在[-3,0]上单调递减.
∵区间[a,8-a]关于x=
| a+8-a |
| 2 |
则由8-a-a>0,解得a<4.
∵-3关于x=4对称的点为x=11,

15关于x=4对称的点为x=-7,
∴要使方程f(x)=0在区间[a,8-a]上恰有3个不同实根,
则11<8-a<15,
解得-7<a<-3,
故答案为:(-7,-3).
点评:本题主要考查函数奇偶性和单调性的应用,利用条件确定函数的周期,利用函数性质的综合应用是解决本题的关键,利用数形结合是解决本题的突破,难度较大,综合性较强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目