题目内容
设x=1和x=2是函数f(x)=x3+ax2+bx+1的两个极值点.
(Ⅰ)求a和b的值;
(Ⅱ)求f(x)的单调区间.
(Ⅰ)求a和b的值;
(Ⅱ)求f(x)的单调区间.
分析:(Ⅰ)三次函数f(x)=x3+ax2+bx+1在x=1和x=2时取极值,说明方程f′(x)=0的两个根为1和2,求出a与b;
(Ⅱ)由(Ⅰ)求出f(x)的解析式,利用导数研究函数的单调性.
(Ⅱ)由(Ⅰ)求出f(x)的解析式,利用导数研究函数的单调性.
解答:解:(Ⅰ)∵三次函数f(x)=x3+ax2+bx+1在x=1和x=2时取极值,
∴f′(x)=3x2+2ax+b,
∴
可得
解得
;
(Ⅱ)由(Ⅰ)知,f′(x)=3x2+2ax+b=3(x-1)(x-2),
若f′(x)>0即x>2或x<1,f(x)为增函数,
若f′(x)<0即1<x<2,f(x)为减函数,
因此f(x)的单调增区间是(-∞,1),(2,+∞),f(x)的单调减区间是(1,2).
∴f′(x)=3x2+2ax+b,
∴
|
|
解得
|
(Ⅱ)由(Ⅰ)知,f′(x)=3x2+2ax+b=3(x-1)(x-2),
若f′(x)>0即x>2或x<1,f(x)为增函数,
若f′(x)<0即1<x<2,f(x)为减函数,
因此f(x)的单调增区间是(-∞,1),(2,+∞),f(x)的单调减区间是(1,2).
点评:此题主要考查函数在某点的极值,利用导数研究函数的单调性,以及掌握不等式的解法.这是高考必考的考点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+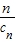 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论; ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.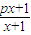 ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+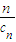 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论;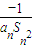 ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.