题目内容
17.已知函数f(x)满足f(x)+1=$\frac{1}{f(x+1)}$,当x∈[0,1]时,f(x)=x,函数g(x)=f(x)-mx-m在[-1,1]内有2个零点,则实数m的取值范围是( )| A. | (0,$\frac{1}{2}$] | B. | (-1,$\frac{1}{2}$] | C. | [$\frac{1}{2},+∞$) | D. | (-∞,$\frac{1}{2}$] |
分析 化简可得当x∈[-1,0)时,f(x)=$\frac{1}{x+1}$-1,从而作出函数y=m(x+1)与函数f(x)在[-1,1]上的图象,从而解得.
解答 解:当x∈[-1,0)时,x+1∈[0,1);
f(x)=$\frac{1}{f(x+1)}$-1=$\frac{1}{x+1}$-1,
从而作出函数y=m(x+1)与函数f(x)在[-1,1]上的图象如下,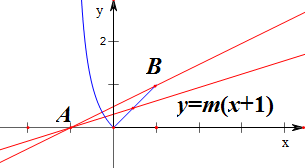
由图象可知,A(-1,0),B(1,1);
故直线AB的斜率kAB=$\frac{1}{2}$,
结合图象可知,
实数m的取值范围是(0,$\frac{1}{2}$];
故选A.
点评 本题考查了数形结合的思想应用.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
5.已知函数f(x)满足f(x)•f(x+2)=1,且f(1)=2,则f(99)=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 99 |
7.在△ABC中,已知sin2A+sin2B-$\sqrt{2}$sinAsinB=sin2C,且满足ab=4$\sqrt{2}$,则该三角形的面积为( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
 设函数y=f(x)是定义在R上的奇函数,当x>0时,f(x)=x2-2x+1,
设函数y=f(x)是定义在R上的奇函数,当x>0时,f(x)=x2-2x+1,