题目内容
12.在区间[-2,3]上任取一个数a,则关于x的方程x2-2ax+a+2=0有根的概率为$\frac{2}{5}$.分析 求出方程x2-2ax+a+2=0有实根的等价条件.利用几何概型的概率公式即可得到结论
解答 解:若方程x2-2ax+a+2=0有实根,
则判别式△=4a2-4(a+2)≥0,
即a2-a-2≥0,解得a≥2或a≤-1,
∵-2≤a≤3,
∴-2≤a≤-1或,2≤a≤3,
则方程x2-2ax+a+2有实根的概率P=$\frac{-1(-2)+3-2}{3-(-2)}$=$\frac{2}{5}$.
故答案为:$\frac{2}{5}$
点评 本题主要考查几何概型的概率的计算,求出方程有根的等价条件是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.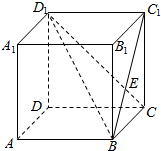 如图,正方体ABCD-A1B1C1D1中,则直线D1C与平面ABC所成角的大小等于( )
如图,正方体ABCD-A1B1C1D1中,则直线D1C与平面ABC所成角的大小等于( )
 如图,正方体ABCD-A1B1C1D1中,则直线D1C与平面ABC所成角的大小等于( )
如图,正方体ABCD-A1B1C1D1中,则直线D1C与平面ABC所成角的大小等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
17.执行如图的程序框图,如果输入的t=0.1,则输出的n=( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
1.已知集合M={x|-2≤x≤2},N={x|x-1>0},则M∩N=( )
| A. | {x|1<x≤2} | B. | {x|-2≤x<1} | C. | {x|1≤x≤2} | D. | {x|x≥-2} |