题目内容
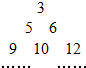 设an是集合2s+2t|0≤s<t,s,t∈Z中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…,将数列an各项按照上小下大、左小右大的原则写成如下的三角形数表:
设an是集合2s+2t|0≤s<t,s,t∈Z中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…,将数列an各项按照上小下大、左小右大的原则写成如下的三角形数表:(1)写出这个三角形数表的第五行的各数;
(2)求a100(可用2s+2t的形式表示);
(3)设bn(n∈N*)是这个三角形数表第n行各数的和,求数列bn的前n项和Sn.
分析:(1)从左到右依次是25+20=33,25+21=34,25+22=36,25+23=40,25+24=48.
(2)第n行有n个数,设a100在第n行,则
+1≤100≤
,由此能求出a100.
(3)依题意,bn=(2n+20)+(2n+21)+…+(2n+2n-1)=(n+1)2n-1,然后由错位相减法能得到前n项和Sn.
(2)第n行有n个数,设a100在第n行,则
| n(n-1) |
| 2 |
| n(n+1) |
| 2 |
(3)依题意,bn=(2n+20)+(2n+21)+…+(2n+2n-1)=(n+1)2n-1,然后由错位相减法能得到前n项和Sn.
解答:解:(1)从左到右依次是25+20=33,
25+21=34,
25+22=36,
25+23=40,
25+24=48.
(2)第n行有n个数,
设a100在第n行,
则
+1≤100≤
,
解得n=14,
100-
=9,
即a100是第14行第9个数,a100=214+28.
(3)依题意,bn=(2n+20)+(2n+21)+…+(2n+2n-1)
=(n+1)2n-1,Sn=b1+b2+bn-1+bn
=(2×21-1)+(3×22-1)+…+(n×2n-1-1)+[(n+1)2n-1]
=[2×21+3×22++n×2n-1+(n+1)2n]-n,2Sn=[2×22+3×23++n×2n+(n+1)2n+1]-2n,两式相减,并由等比数列前n项和公式得Sn=-2×21-[22+23+…+2n]+(n+1)2n+1-n
=n×(2n+1-1).
25+21=34,
25+22=36,
25+23=40,
25+24=48.
(2)第n行有n个数,
设a100在第n行,
则
| n(n-1) |
| 2 |
| n(n+1) |
| 2 |
解得n=14,
100-
| n(n-1) |
| 2 |
即a100是第14行第9个数,a100=214+28.
(3)依题意,bn=(2n+20)+(2n+21)+…+(2n+2n-1)
=(n+1)2n-1,Sn=b1+b2+bn-1+bn
=(2×21-1)+(3×22-1)+…+(n×2n-1-1)+[(n+1)2n-1]
=[2×21+3×22++n×2n-1+(n+1)2n]-n,2Sn=[2×22+3×23++n×2n+(n+1)2n+1]-2n,两式相减,并由等比数列前n项和公式得Sn=-2×21-[22+23+…+2n]+(n+1)2n+1-n
=n×(2n+1-1).
点评:(1)是将数表的排列“规律”具体运用到某一行;(2)是探讨an和s、t的联系;(3)从已知数列中分离或错位相减构造出等差(等比)数列,再运用等差(等比)数列的性质求解.

练习册系列答案
相关题目