题目内容
每年的三月十二日,是中国的植树节,林管部门在植树前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲、乙两种树苗中各抽测了10株树苗的高度,规定高于128厘米的树苗为“良种树苗”,测得高度如下(单位:厘米):
甲:137,121,131,120,129,119,132,123,125,133;
乙:110,130,147,127,146,114,126,110,144,146.
(1)根据抽测结果,画出甲、乙两种树苗高度的茎叶图,并根据你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出对两种树苗高度的统计结论;
(2)设抽测的10株甲种树苗高度平均值为x,将这10株树苗的高度依次输入按程序框图进行运算(如图),问输出的S大小为多少?并说明S的统计学意义;
(3)若小王在甲种树苗中随机领取了5株进行种植,用样本的频率分布估计总体分布,求小王领取到的“良种树苗”的株数X的分布列.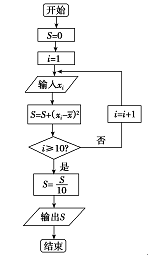
(1)参考解析; (2)35,方差;(3)参考解析
解析试题分析:(1)根据已知的数据画出甲、乙两种树苗高度的茎叶图,通过茎叶图从几个统计知识方面可得到两种数高的比较,比如树苗的平均高度;长得更整齐度;中位数的值;高度基本上是对称的,而且大多数集中在均值附近.
(2)由程序框图可知,其运算的结果是这十棵树苗的方差,方差s表示的统计的意义为描述树苗高度的离散程度的量.S值越小,表示树苗长得越整齐,S值越大,表示树苗长得越参差不齐.
(3)在甲种树苗中随机领取了5株进行种植,取到的“良种树苗”的株数X同有0,1,2,3,4,5这六种情况,所以可列出X的分布列.
(1)茎叶图如图所示:(2分)甲 乙 9
0 1 3 5 9
1 2 3 711
12
13
140 0 4
6 7
0
4 6 6 7
统计结论:①甲种树苗的平均高度小于乙种树苗的平均高度;
②甲种树苗比乙种树苗长得更整齐;
③甲种树苗高度的中位数为127,乙种树苗高度的中位数为128.5;
④甲种树苗的高度基本上是对称的,而且大多数集中在均值附近,乙种树苗的高度分布较为分散 4分(每写出一个统计结论得1分)
(2)依题意,x=127,S=35. (6分)
S表示10株甲种树苗高度的方差,是描述树苗高度的离散程度的量.S值越小,表示树苗长得越整齐,S值越大,表示树苗长得越参差不齐.
(3)由题意可知,领取一株甲种树苗得到“良种树苗”的概率为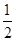 ,则X~B
,则X~B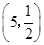 , (10分)
, (10分)
所以随机变量X的分布列为
13分X 0 1 2 3 4 5 P 
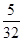


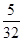

考点:1.统计的知识.2.概率的知识.3.茎叶图.4.分布列问题.

随机观测生产某种零件的某工厂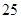 名工人的日加工零件数(单位:件),获得数据如下:
名工人的日加工零件数(单位:件),获得数据如下: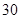 、
、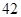 、
、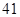 、
、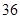 、
、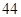 、
、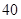 、
、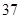 、
、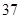 、
、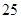 、
、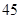 、
、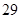 、
、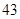 、
、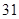 、
、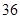 、
、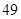 、
、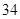 、
、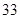 、
、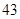 、
、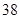 、
、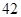 、
、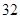 、
、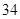 、
、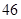 、
、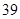 、
、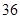 ,根据上述数据得到样本的频率分布表如下:
,根据上述数据得到样本的频率分布表如下:
| 分组 | 频数 | 频率 |
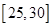 | 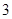 | 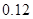 |
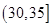 |  |  |
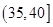 | 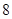 | 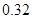 |
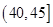 | 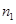 | 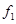 |
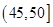 | 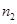 | 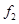 |
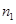 、
、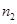 、
、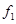 和
和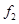 的值;
的值;(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布直方图,求在该厂任取
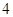 人,至少有
人,至少有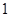 人的日加工零件数落在区间
人的日加工零件数落在区间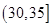 的概率.
的概率. (13分)(2011•陕西)如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到火车站的人进行调查,调查结果如下:
| 所用时间(分钟) | 10~20 | 20~30 | 30~40 | 40~50 | 50~60 |
| 选择L1的人数 | 6 | 12 | 18 | 12 | 12 |
| 选择L2的人数 | 0 | 4 | 16 | 16 | 4 |

(Ⅰ)试估计40分钟内不能 赶到火车站的概率;
(Ⅱ)分别求通过路径L1和L2所用时间落在上表中各时间段内的频率;
(Ⅲ)现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站,为了尽量大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的 路径.
近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重,大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对入院的50人进行了问卷调查得到了如下的列联表:
| | 患心肺疾病 | 不患心肺疾病 | 合计 |
| 男 | | 5 | |
| 女 | 10 | | |
| 合计 | | | 50 |
已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由;
临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:
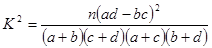 其中
其中
甲、乙两名射手在一次射击中的得分为两个相互独立的随机变量ξ和η,且ξ、η分布列为
| ξ | 1 | 2 | 3 |
| P | a | 0.1 | 0.6 |
| η | 1 | 2 | 3 |
| P | 0.3 | b | 0.3 |
(2)计算ξ、η的期望和方差,并以此分析甲、乙的技术状况.
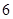 道备选题中一次性随机抽取
道备选题中一次性随机抽取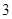 道题,按照题目要求独立完成.规定:至少正确完成其中
道题,按照题目要求独立完成.规定:至少正确完成其中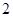 道题的便可通过.已知
道题的便可通过.已知 道题能正确完成,
道题能正确完成,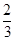 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.