题目内容
(本小题满分9分)一个袋子中有3个红球和2个黄球，5个球除颜色外完全相同，甲、乙两人先后不放回地从中各取1个球.规定：若两人取得的球的颜色相同则甲获胜，否则乙获胜.
(1) 求两个人都取到黄球的概率；
(2) 计算甲获胜的概率.
(1)
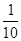;(2)
.
解析试题分析：(1) 设3个红球编号为1、2、3；两个黄球编号为4、5,分别列出甲乙两人先后不放回地各取一个球的所有基本事件
，然后找到其中的两人都取到黄球的事件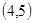
,
;
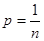(2)甲获胜指的是两人取到相同颜色的球，即两个红的或是两个黄的.看其中有几个基本事件
，
.
解：设3个红球编号为1、2、3；两个黄球编号为4、5.则一切可能结果组成的基本事件有（1,2）、（1,3）、（1，4）、（1,5）、（2,3）、（2,4）、（2,5）、（3,4）、（3,5）、（4,5）共10个。 （2分）
两个人都取得黄球的事件有（4,5）共1个。因此两个人都取得黄球概率为P=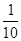
（6分（注意格式，要设事件，要作答））
（2）两个人取得相同颜色球的事件有（1,2）、（1,3）、（2,3）、（4,5）共4个
故甲获胜的概率为P=
. （9分（注意格式，要设事件，要作答））
考点：古典概型的概率问题
千里马走向假期期末仿真试卷寒假系列答案一个袋中装有8个大小质地相同的球，其中4个红球、4个白球，现从中任意取出四个球，设X为取得红球的个数．
（1）求X的分布列；
（2）若摸出4个都是红球记5分，摸出3个红球记4分，否则记2分．求得分的期望．
（2013•重庆）某商场举行的“三色球”购物摸奖活动规定：在一次摸奖中，摸奖者先从装有3个红球与4个白球的袋中任意摸出3个球，再从装有1个蓝球与2个白球的袋中任意摸出1个球，根据摸出4个球中红球与蓝球的个数，设一、二、三等奖如下：
| 奖级 | 摸出红、蓝球个数 | 获奖金额 |
| 一等奖 | 3红1蓝 | 200元 |
| 二等奖 | 3红0蓝 | 50元 |
| 三等奖 | 2红1蓝 | 10元 |
其余情况无奖且每次摸奖最多只能获得一个奖级．
（1）求一次摸奖恰好摸到1个红球的概率；
（2）求摸奖者在一次摸奖中获奖金额x的分布列与期望E（x）．
甲、乙二人参加知识竞答，共有10个不同的题目，其中选择题6个，判断题4个，甲、乙二人依次各抽一题,那么
(1)甲抽到选择题，乙抽到判断题的概率是多少?
(2)甲、乙二人中至少有一个抽到选择题的概率是多少?
，每道程序中得优、良、中的概率分别为p1、
、p2.(2014·郑州模拟)某学生对其30位亲属的饮食习惯进行了一次调查,并用茎叶图表示30人的饮食指数.说明：如图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.
(1)根据茎叶图,帮助这位同学说明其亲属30人的饮食习惯.
(2)根据以上数据完成2×2列联表：
| | 主食蔬菜 | 主食肉类 | 总计 |
| 50岁以下 | | | |
| 50岁以上 | | | |
| 总计 | | | |