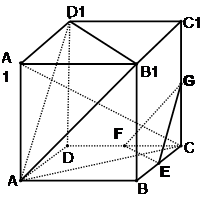题目内容
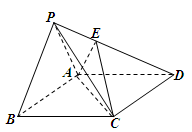
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.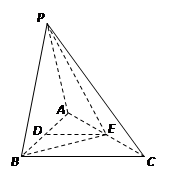
(Ⅰ)求证:DE∥平面PBC;
(Ⅱ)求证:AB⊥PE;
(Ⅲ)求二面角A-PB-E的大小.
(Ⅰ)由D、E分别为AB、AC中点,得DE∥BC .可得DE∥平面PBC
(Ⅱ)连结PD,由PA=PB,得PD ⊥ AB. DE∥BC,BC ⊥ AB,推出DE ⊥ AB.
AB⊥平面PDE,得到AB⊥PE .
(Ⅲ)证得PD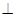 平面ABC 。
平面ABC 。
以D为原点建立空间直角坐标系。
二面角的A-PB-E的大小为 .
.
解析试题分析:(Ⅰ)D、E分别为AB、AC中点,\DE∥BC .
DEË平面PBC,BCÌ平面PBC,∴DE∥平面PBC
(Ⅱ)连结PD, PA=PB,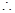 PD ⊥ AB. DE∥BC,BC ⊥ AB,
PD ⊥ AB. DE∥BC,BC ⊥ AB,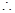 DE ⊥ AB.又
DE ⊥ AB.又
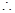 AB⊥平面PDE,PEÌ平面PDE,
AB⊥平面PDE,PEÌ平面PDE,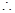 AB⊥PE . 6分
AB⊥PE . 6分
(Ⅲ)平面PAB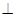 平面ABC,平面PAB
平面ABC,平面PAB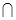 平面ABC=AB,PD
平面ABC=AB,PD 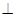 AB,
AB,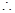 PD
PD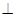 平面ABC. 7分
平面ABC. 7分
如图,以D为原点建立空间直角坐标系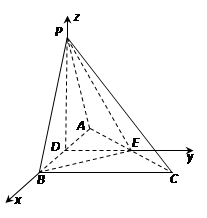
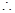 B(1,0,0),P(0,0,
B(1,0,0),P(0,0,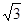 ),E(0,
),E(0,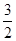 ,0) ,
,0) ,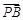 =(1,0,
=(1,0,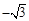 ),
),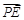 ="(0,"
="(0," 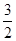 ,
, 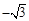 ).
).
设平面PBE的法向量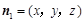 ,
,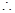
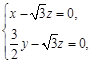
令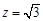 得
得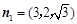 .
.
DE⊥平面PAB,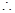 平面PAB的法向量为
平面PAB的法向量为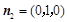 .
.
设二面角的A-PB-E大小为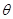
由图知,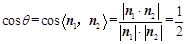 ,
,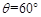 ,
,
二面角的A-PB-E的大小为 .
.
考点:立体几何中的平行关系、垂直关系,角的计算,空间向量的应用。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,本题利用空间向量,简化了证明及计算过程。

 名校课堂系列答案
名校课堂系列答案经过两直线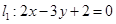 与
与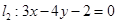 的交点,且平行于直线
的交点,且平行于直线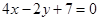 的直线方程是( ).
的直线方程是( ).
A.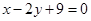 | B.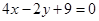 |
C.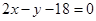 | D.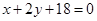 |
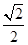 AB.
AB.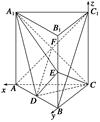
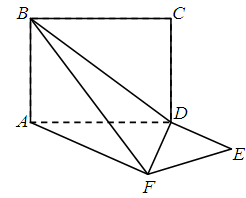
 ,求AB的长.
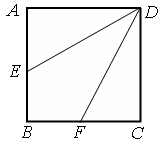
,求AB的长.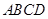 中,点
中,点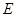 是
是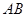 的中点,点
的中点,点 是
是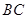 的中点,将△
的中点,将△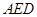 、△
、△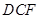 分别沿
分别沿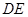 、
、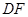 折起,使
折起,使 、
、 两点重合于点
两点重合于点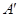 ,连接
,连接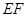 ,
,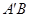 .
.
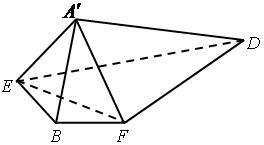
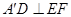 ;
;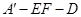 的余弦值.
的余弦值.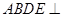 平面
平面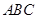 ,
,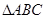 是等腰直角三角形,
是等腰直角三角形,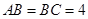 ,四边形
,四边形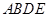 是直角梯形,
是直角梯形,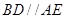 ,
,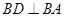 ,
,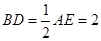 ,点
,点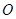 、
、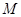 分别为
分别为 、
、 的中点.
的中点.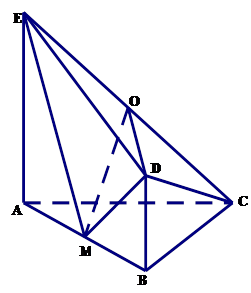
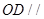 平面
平面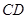 和平面
和平面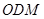 所成角的正弦值;
所成角的正弦值;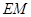 上找到一点
上找到一点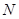 ,使得
,使得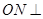 平面
平面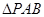 为边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,
为边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,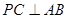 ,E为PD点上一点,满足
,E为PD点上一点,满足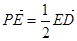
 平面ABCD;
平面ABCD;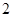 的正方体
的正方体 中,
中, 、
、 分别是
分别是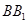 、
、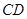 的中点,试用向量的方法:
的中点,试用向量的方法: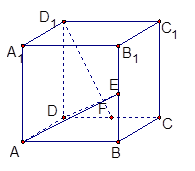
 求证:
求证: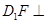 平面
平面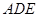 ;
; 求
求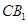 与平面
与平面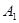 C与平面ABCD所成角的正弦的值;
C与平面ABCD所成角的正弦的值;