题目内容
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,离心率为
,离心率为![]() , 点
, 点![]() 在椭圆上且位于第一象限,直线
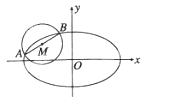
在椭圆上且位于第一象限,直线![]() 被圆
被圆![]() 截得的线段的长为
截得的线段的长为![]() .(1)求直线 F M 的斜率(2)求椭圆的方程(3)设动点 P 在椭圆上,若直线FP的斜率大于
.(1)求直线 F M 的斜率(2)求椭圆的方程(3)设动点 P 在椭圆上,若直线FP的斜率大于![]() ,求直线OP( O 为原点)的斜率的取值范围
,求直线OP( O 为原点)的斜率的取值范围
(1)求直线![]() 的斜率
的斜率
(2)求椭圆的方程
(3)设动点![]() 在椭圆上,若直线
在椭圆上,若直线![]() 的斜率大于
的斜率大于![]() , 求直线
, 求直线![]() (
(![]() 为原点)的斜率的取值范围
为原点)的斜率的取值范围
【答案】
(1)
![]()
(2)
![]()
(3)
![]()
【解析】(1)由已知有![]() , 又由
, 又由![]() ,可得
,可得![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() , 由已知有
, 由已知有![]() ,解得
,解得![]()
(2)由(1)得椭圆方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,两个方程联立,消去
,两个方程联立,消去![]() , 整理得
, 整理得![]() , 解得
, 解得![]() 或
或![]() , 因为点
, 因为点![]() 在第一象限,可得
在第一象限,可得![]() 的坐标为
的坐标为![]() , 由
, 由![]() ,解得
,解得![]() , 所以椭圆方程为
, 所以椭圆方程为![]()
(3)设点![]() 的坐标为
的坐标为![]() , 直线
, 直线![]() 的斜率为
的斜率为![]() , 得
, 得![]() ,即
,即![]() ,与椭圆方程联立
,与椭圆方程联立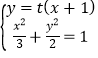 ,消去
,消去![]() ,整理得
,整理得![]() ,又由已知,得
,又由已知,得![]() ,解得
,解得![]() 或
或![]() , 设直线
, 设直线![]() 的斜率为
的斜率为![]() , 得
, 得![]() , 即
, 即![]() , 与椭圆方程联立,整理可得
, 与椭圆方程联立,整理可得![]() , 当
, 当![]() 时,有
时,有![]() ,因此
,因此![]() , 于是
, 于是![]() ,得
,得![]() ;当
;当![]() 时,有
时,有![]() ,因此
,因此![]() ,于是
,于是![]() ,得
,得![]() 综上,直线
综上,直线![]() 的斜率的取值范围是
的斜率的取值范围是![]()
【考点精析】利用椭圆的标准方程对题目进行判断即可得到答案,需要熟知椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目