题目内容
已知在△ABC中,(1)若三边长a,b,c依次成等差数列,sinA:sinB=3:5,求三个内角中最大角的度数;
(2)若
 ,求cosB.
,求cosB.
【答案】分析:(1)依题意,设a=3k,(k>0),则b=5k,c=7k,利用余弦定理即可求得三个内角中最大角的度数;
(2)利用向量的数量积,与余弦定理即可求得cosB.
解答:解:(1)在△ABC中有sinA:sinB=3:5,
∴a:b=3:5,设a=3k,(k>0)
则b=5k,
∵a,b,c成等差数列,
∴c=7k,
∴最大角为C,有cosC=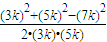 =-
=- ,
,
∴C=120°
(2)由 •
• =b2-(a-c)2 得:accosB=b2-(a-c)2,
=b2-(a-c)2 得:accosB=b2-(a-c)2,
即accosB=a2+c2-2accosB-(a2+c2-2ac),
∴3cosB=2,
∴cosB= .
.
点评:本题考查余弦定理,考查平面向量的数量积,考查运算能力,属于中档题.
(2)利用向量的数量积,与余弦定理即可求得cosB.
解答:解:(1)在△ABC中有sinA:sinB=3:5,
∴a:b=3:5,设a=3k,(k>0)
则b=5k,
∵a,b,c成等差数列,
∴c=7k,
∴最大角为C,有cosC=
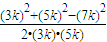 =-
=- ,
,∴C=120°
(2)由
 •
• =b2-(a-c)2 得:accosB=b2-(a-c)2,
=b2-(a-c)2 得:accosB=b2-(a-c)2,即accosB=a2+c2-2accosB-(a2+c2-2ac),
∴3cosB=2,
∴cosB=
 .
.点评:本题考查余弦定理,考查平面向量的数量积,考查运算能力,属于中档题.

练习册系列答案
相关题目