题目内容
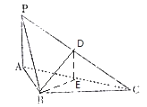
【题目】如图,四面体![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在,求
,若存在,求![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】(Ⅰ)详见解析;(Ⅱ)在线段![]() 上存在点
上存在点![]() ,当
,当![]() 时,使得
时,使得![]() .
.
【解析】
(Ⅰ)由勾股定理得![]() ,又
,又![]() 平面
平面![]() ,可证
,可证![]() ,利用线面垂直的判定定理即可得到证明;(Ⅱ)在平面
,利用线面垂直的判定定理即可得到证明;(Ⅱ)在平面![]() 内,过点
内,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,在平面
,在平面![]() 内,过点
内,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() ,利用线面垂直的判断定理可证
,利用线面垂直的判断定理可证![]() 平面
平面![]() ,利用线面垂直的性质可证
,利用线面垂直的性质可证![]() ,在
,在![]() 中,解三角形即可得解
中,解三角形即可得解![]() 的值.
的值.
(Ⅰ)由题知:![]() ,
,![]() ,
,![]() .
.
则![]() ,所以
,所以![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() ,
,
所以![]() 平面
平面![]() ;
;
(Ⅱ)在线段![]() 上存在点
上存在点![]() ,当
,当![]() 时,使得
时,使得![]() .
.
理由如下:
在平面![]() 内,过点
内,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
在平面![]() 内,过点
内,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() ,
,
由![]() 平面
平面![]() ,知
,知![]() ,
,
所以![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
在![]() 中,
中,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,![]()

【题目】为了保障全国第四次经济普查顺利进行,国家统计局从东部选择江苏,从中部选择河北. 湖北,从西部选择宁夏,从直辖市中选择重庆作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区.在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记.由于种种情况可能会导致入户登记不够顺利,这为正式普查提供了宝贵的试点经验.在某普查小区,共有 50 家企事业单位,150 家个体经营户,普查情况如下表所示:
普查对象类别 | 顺利 | 不顺利 | 合计 |
企事业单位 | 40 | 50 | |
个体经营户 | 50 | 150 | |
合计 |
(1)写出选择 5 个国家综合试点地区采用的抽样方法;
(2)补全上述列联表(在答题卡填写),并根据列联表判断是否有![]() 的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
(3)根据该试点普查小区的情况,为保障第四次经济普查的顺利进行,请你从统计的角度提出一条建议.
附:![]()
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
【题目】对某电子元件进行寿命追踪调查,情况如下:
寿命分组/h | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
个数 | 20 | 30 | 80 | 40 | 30 |
(1)求下表中的x,y;
寿命分组/h | 频数 | 频率 |
100~200 | 20 | 0.10 |
200~300 | 30 | x |
300~400 | 80 | 0.40 |
400~500 | 40 | 0.20 |
500~600 | 30 | y |
合计 | 200 | 1 |
(2)从频率分布直方图估计电子元件寿命的第80百分位数是多少.