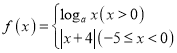题目内容
【题目】已知![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)求![]() 时,
时,![]() 的值域:
的值域:
(3)设![]() ,若
,若![]() 对任意的
对任意的![]() ,总有
,总有![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】(1)![]() ;(2)当
;(2)当![]() 时
时![]() 的值域为
的值域为![]() ;当
;当![]() 时
时![]() 的值域为
的值域为![]() ;(3)
;(3)![]() .
.
【解析】
(1)使用换元法令![]() 即可得解;
即可得解;
(2)令![]()
![]() ,则
,则![]() ,根据
,根据![]() 的取值结合一次函数、二次函数的性质即可得解.
的取值结合一次函数、二次函数的性质即可得解.
(3)转化条件为![]() .令
.令![]() 得
得![]() ,根据
,根据![]() 的范围讨论
的范围讨论![]() 时函数
时函数![]() 的最值即可得解.
的最值即可得解.
(1)设![]() ,则
,则![]() ,所以
,所以![]()
所以![]() ;
;
(2)设![]() ,
,![]() ,则
,则![]() ,
,
所以![]()
当![]() 时,
时,![]() ,
,![]() 的值域为
的值域为![]()
当![]() 时,
时,![]()
若![]() ,对称轴
,对称轴![]() ,
,![]() 的值域为
的值域为![]() ,
,
若![]() ,对称轴
,对称轴![]() ,
,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,![]() 的值域为
的值域为![]() .
.
综上,当![]() 时
时![]() 的值域为
的值域为![]() ;当
;当![]() 时
时![]() 的值域为
的值域为![]() .
.
(3)化简得![]() ,
,
对任意![]() 总有
总有![]() ,
,
∴![]() 在
在![]() 满足
满足![]() .
.
设![]() ,则
,则![]() ,
,
当![]() 即
即![]() 时
时![]() 在区间
在区间![]() 单调递增,
单调递增,
所以![]() ,即
,即![]() ,所以
,所以![]() ,则
,则![]()
当![]() 时,下证函数
时,下证函数![]() 在区间
在区间![]() 单调递增:
单调递增:
任取![]() ,
,
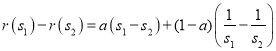
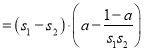 ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
又 ![]() ∴
∴![]() 即函数
即函数![]() 在区间
在区间![]() 单调递增,
单调递增,
又 ![]() 时,
时,![]() 恒成立,∴
恒成立,∴![]() 满足要求.
满足要求.
综上![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某生产企业研发了一种新产品,该新产品在某网店试销一个阶段后得到销售单价![]() 和月销售量
和月销售量![]() 之间的一组数据,如下表所示:
之间的一组数据,如下表所示:
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(1)根据统计数据,求出![]() 关于
关于![]() 的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
(2)生产企业与网店约定:若该新产品的月销售量不低于10万件,则生产企业奖励网店1万元;若月销售量不低于8万件且不足10万件,则生产企业奖励网店5000元;若月销售量低于8万件,则没有奖励.现用样本估计总体,从上述5个销售单价中任选2个销售单价,下个月分别在两个不同的网店进行销售,求这两个网店下个月获得奖励的总额![]() 的分布列及其数学期望.
的分布列及其数学期望.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为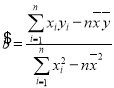 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.