题目内容

已知椭圆左、右焦点分别为F1、F2，点，点F2在线段PF1的中垂线上。

   （1）求椭圆C的方程；（8分）

   （2）设直线与椭圆C交于M、N两点，直线F2M与F2N的倾斜角分别为，且，求证：直线过定点，并求该定点的坐标。（12分）

 

解析： （1）（8分）由椭圆C的离心率 w.w.w.k.s.5.u.c.o.m          

       得，其中，

       椭圆C的左、右焦点分别为

       又点F2在线段PF1的中垂线上

      

       解得           

   （2）（12分）由题意，知直线MN存在斜率，设其方程为

       由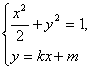

       消去

       设

       则

       且   8分

       由已知，

       得 w.w.w.k.s.5.u.c.o.m          

       化简，得     10分

      

       整理得

直线MN的方程为，     

       因此直线MN过定点，该定点的坐标为（2，0）
练习册系列答案
相关题目
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0），其焦距为2c，若
c
a
=
5
-1
2
（≈0.618），则称椭圆C为“黄金椭圆”．
（1）求证：在黄金椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）中，a、b、c成等比数列．
（2）黄金椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的右焦点为F2（c，0），P为椭圆C上的任意一点．是否存在过点F2、P的直线l，使l与y轴的交点R满足
RP
=-3
PF2
？若存在，求直线l的斜率k；若不存在，请说明理由．
（3）在黄金椭圆中有真命题：已知黄金椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别是F1（-c，0）、F2（c，0），以A（-a，0）、B（a，0）、D（0，-b）、E（0，b）为顶点的菱形ADBE的内切圆过焦点F1、F2．试写出“黄金双曲线”的定义；对于上述命题，在黄金双曲线中写出相关的真命题，并加以证明．
已知中心在坐标原点、焦点在x轴上椭圆的离心率e=
3
3
，以原点为圆心，椭圆的短半轴长为半径的圆与直线y=x+2相切．
（1）求该椭圆的标准方程；
（2）设椭圆的左，右焦点分别是F1和F2，直线l1过F2且与x轴垂直，动直线l2与y轴垂直，l2交l1于点P，求线段PF1的垂直平分线与l2的交点M的轨迹方程，并指明曲线类型．
（2012•茂名二模）已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别是F1（-c，0）、F2（c，0），离心率为
1
2
，椭圆上的动点P到直线l：x=
a2
c
的最小距离为2，延长F2P至Q使得|
F2Q
|=2a，线段F1Q上存在异于F1的点T满足
PT
•
TF1
=0．
（1）求椭圆的方程；
（2）求点T的轨迹C的方程；
（3）求证：过直线l：x=
a2
c
上任意一点必可以作两条直线与T的轨迹C相切，并且过两切点的直线经过定点．
已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为
2
2
，左、右焦点分别是F1，F2，过点F1的直线l交C于A，B两点，且△ABF2的周长为4
2
．则椭圆C的方程为
 
．

（本小题满分12分）

已知椭圆左、右焦点分别为F1、F2，点，点F2在线段PF1的中垂线上。

（1）求椭圆C的方程；

（2）设直线与椭圆C交于M、N两点，直线F2M与F2N的倾斜角互补，求证：直线过定点，并求该定点的坐标。

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网