题目内容
本题A、B、C三个选答题,请考生任选一题作答,如果多做,则按所做的第一题计分.A.(不等式选讲选做题)若不等式|x-1|+|x-m|<2m的解集为∅,则m的取值范围为 .
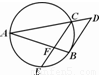
B.(几何证明选讲选做题)如图所示,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于点D.过点C作BD的平行线与圆相交于点E,与AB相交于点F,AF=3,FB=1,EF=
 ,则线段CD的长为 .
,则线段CD的长为 .C.(极坐标系与参数方程选做题)在极坐标系中,ρ(2,
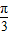 )的直角坐标是 .
)的直角坐标是 .
【答案】分析:A.由题意可得|x-1|+|x-m|的最小值|m-1|>2m,即m-1>2m,或 m-1<-2m,由此求得m的取值范围.
B.由相交弦定理求出FC,由相似比求出BD,设DC=x,则AD=4x,再由切割线定理,BD2=CD•AD求解.
C.直接根据公式 x=ρcosθ,y=ρsinθ,把点的极坐标化为直角坐标.
解答:解:A.∵不等式|x-1|+|x-m|<2m的解集为∅,而由绝对值的意义可得|x-1|+|x-m|的最小值为|m-1|,
∴|m-1|>2m,∴m-1>2m,或 m-1<-2m. 解得 m≤ ,
,
故答案为 (-∞, ].
].
B.由相交弦定理得到AF•FB=EF•FC,即3×1= ×FC,FC=2,在△ABD中,AF:AB=FC:BD,即3:4=2:BD,BD=
×FC,FC=2,在△ABD中,AF:AB=FC:BD,即3:4=2:BD,BD= ,
,
设DC=x,则AD=4x,再由切割线定理,BD2=CD•AD,即x•4x=( )2,解得 x=
)2,解得 x= ,
,
故答案为: .
.
C.在极坐标系中,∵点的极坐标 ρ(2,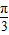 ),设它的直角坐标(x,y),
),设它的直角坐标(x,y),
则 x=2cos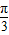 =1,y=2sin
=1,y=2sin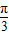 =
=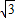 ,故设它的直角坐标(1,
,故设它的直角坐标(1,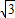 ),
),
故答案为 (1,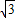 ).
).
点评:本题主要考查绝对值不等式的解法,直线与圆的位置关系,相交弦定理,切割线定理,相似三角形的概念、判定与性质,点的极坐标化为直角坐标的方法,属于基础题.
B.由相交弦定理求出FC,由相似比求出BD,设DC=x,则AD=4x,再由切割线定理,BD2=CD•AD求解.
C.直接根据公式 x=ρcosθ,y=ρsinθ,把点的极坐标化为直角坐标.
解答:解:A.∵不等式|x-1|+|x-m|<2m的解集为∅,而由绝对值的意义可得|x-1|+|x-m|的最小值为|m-1|,
∴|m-1|>2m,∴m-1>2m,或 m-1<-2m. 解得 m≤
 ,
,故答案为 (-∞,
 ].
].B.由相交弦定理得到AF•FB=EF•FC,即3×1=
 ×FC,FC=2,在△ABD中,AF:AB=FC:BD,即3:4=2:BD,BD=
×FC,FC=2,在△ABD中,AF:AB=FC:BD,即3:4=2:BD,BD= ,
,设DC=x,则AD=4x,再由切割线定理,BD2=CD•AD,即x•4x=(
 )2,解得 x=
)2,解得 x= ,
,故答案为:
 .
.C.在极坐标系中,∵点的极坐标 ρ(2,
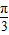 ),设它的直角坐标(x,y),
),设它的直角坐标(x,y),则 x=2cos
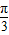 =1,y=2sin
=1,y=2sin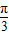 =
=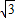 ,故设它的直角坐标(1,
,故设它的直角坐标(1,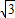 ),
),故答案为 (1,
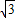 ).
).点评:本题主要考查绝对值不等式的解法,直线与圆的位置关系,相交弦定理,切割线定理,相似三角形的概念、判定与性质,点的极坐标化为直角坐标的方法,属于基础题.

练习册系列答案
相关题目
 本题A、B、C三个选答题,请考生任选一题作答,如果多做,则按所做的第一题计分.
本题A、B、C三个选答题,请考生任选一题作答,如果多做,则按所做的第一题计分. ,则线段CD的长为 .
,则线段CD的长为 .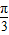 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 .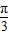 )的直角坐标是 .
)的直角坐标是 .