题目内容
（文科做）已知直线l过点P（2，1），且与x轴、y轴的正半轴分别交于A、B两点，O为坐标原点，则三角形OAB面积的最小值为（ ）A．1
B．2
C．3
D．4
【答案】分析：设出直线的截距式方程，推出截距关系式，写出面积的表达式，再由不等式得最值．
解答：解：设直线l为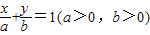
，
因为直线l过点P（2，1），则有关系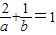
．
△OAB面积为S=
对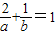
，利用均值不等式，
得1=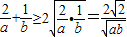
，即ab≥8．
于是，△OAB面积为S=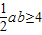
．
故选D．
点评：本题考查直线方程，基本不等式的应用，设出适当的直线方程，可使问题简化，得出解答．
解答：解：设直线l为
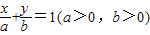，因为直线l过点P（2，1），则有关系
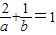．△OAB面积为S=
对
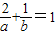，利用均值不等式，得1=
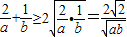，即ab≥8．于是，△OAB面积为S=
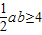．故选D．
点评：本题考查直线方程，基本不等式的应用，设出适当的直线方程，可使问题简化，得出解答．
练习册系列答案
相关题目