题目内容
已知m、n是两条不同的直线,α、β是两个不同的平面,给出下列命题:
①若α⊥β,m∥α,则m⊥β;
②若m⊥α,n⊥β,且m⊥n,则α⊥β;
③若m⊥β,m∥α,则α⊥β;
④若m∥α,n∥β,且m∥n,则α∥β.
其中正确命题的序号是( )
①若α⊥β,m∥α,则m⊥β;
②若m⊥α,n⊥β,且m⊥n,则α⊥β;
③若m⊥β,m∥α,则α⊥β;
④若m∥α,n∥β,且m∥n,则α∥β.
其中正确命题的序号是( )
分析:对于①当α⊥β,m∥α时,m⊥β不一定成立;
对于②可以看成m是平面α的法向量,n是平面β的法向量即可;
对于③可由面面垂直的判断定理作出判断;
对于④m∥α,n∥β,且m∥n,α,β也可能相交.
对于②可以看成m是平面α的法向量,n是平面β的法向量即可;
对于③可由面面垂直的判断定理作出判断;
对于④m∥α,n∥β,且m∥n,α,β也可能相交.
解答:解:①当α⊥β,m∥α时,m⊥β不一定成立,所以错误;
②利用当两个平面的法向量互相垂直时,这两个平面垂直,故成立;
③因为m∥α,则一定存在直线n在β,使得m∥n,又m⊥β可得出n⊥β,由面面垂直的判定定理知,α⊥β,故成立;
④m∥α,n∥β,且m∥n,α,β也可能相交,如图所示,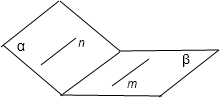 ,所以错误,
,所以错误,
故选B.
②利用当两个平面的法向量互相垂直时,这两个平面垂直,故成立;
③因为m∥α,则一定存在直线n在β,使得m∥n,又m⊥β可得出n⊥β,由面面垂直的判定定理知,α⊥β,故成立;
④m∥α,n∥β,且m∥n,α,β也可能相交,如图所示,
 ,所以错误,
,所以错误,故选B.
点评:本题以命题的真假判断为载体考查了空间直线与平面的位置关系,熟练掌握空间线面关系的判定及几何特征是解答的关键.

练习册系列答案
相关题目