题目内容
(本题满分12分)设正项数列 的前
的前 项和
项和 ,且满足
,且满足 .
.
(Ⅰ)计算 的值,猜想
的值,猜想 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;
(Ⅱ)设 是数列
是数列 的前
的前 项和,证明:
项和,证明: .
.
【答案】
(Ⅰ)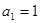 ;
;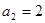 ;
;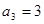 .猜想
.猜想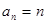 ,用数学归纳法证明;(Ⅱ)先利用数列知识求和,然后利用放缩法证明或者利用数学归纳法证明
,用数学归纳法证明;(Ⅱ)先利用数列知识求和,然后利用放缩法证明或者利用数学归纳法证明
【解析】
试题分析:(Ⅰ)当n=1时,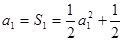 ,得
,得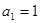 ;
;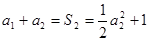 ,得
,得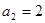 ;
;
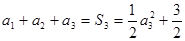 ,得
,得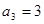 .猜想
.猜想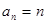 2’
2’
证明:(ⅰ)当n=1时,显然成立.
(ⅱ)假设当n=k时,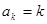 1’
1’
则当n=k+1时,
结合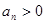 ,解得
,解得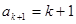 2’
2’
于是对于一切的自然数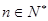 ,都有
,都有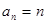 1’
1’
(Ⅱ)证法一:因为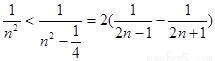 ,
3’
,
3’
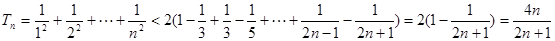 .3’
.3’
证法二:数学归纳法
证明:(ⅰ)当n=1时,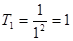 ,
,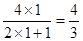 ,
,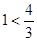 1’
1’
(ⅱ)假设当n=k时,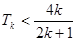 1’
1’
则当n=k+1时,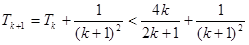
要证: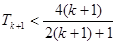
只需证: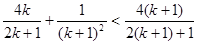
由于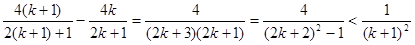
所以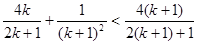 3’
3’
于是对于一切的自然数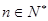 ,都有
,都有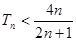 1’
1’
考点:本题考查了数学归纳法的运用
点评:运用数学归纳法,可以证明下列问题:与自然数n有关的恒等式、代数不等式、三角不等式、数列问题、几何问题、整除性问题等等。

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 :实数
:实数 满足
满足 , 命题
, 命题 :实数
:实数 .
. 为真,求实数
为真,求实数 .
. 的单调区间;
的单调区间; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,其中
,其中 。
。 时,求不等式
时,求不等式 的解集;
的解集;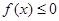 的解集为
的解集为 ,求a的值。
,求a的值。
 与
与 垂直,求
垂直,求 的值
的值  的最大值;
的最大值;  ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 与
与 、
、 两点,且
两点,且 ,
, ,
, 成等差数列,
成等差数列, 满足
满足 ,求
,求