题目内容
(本小题满分12分)
如图,在梯形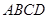 中,
中, ∥
∥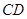 ,
,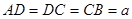 ,
,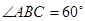 ,平面
,平面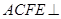 平面
平面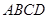 ,四边形
,四边形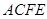 是矩形,
是矩形,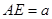 ,点
,点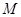 在线段
在线段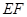 上.
上.

(1)求证:平面BCF⊥平面ACFE;
(2)当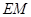 为何值时,
为何值时,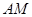 ∥平面
∥平面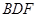 ?证明你的结论;
?证明你的结论;
【答案】
(Ⅰ)见解析;(Ⅱ)当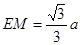 时,
时,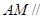 平面
平面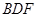
【解析】本题考查线面位置关系及判定,考查空间想象能力,计算能力,转化能力
(Ⅰ)由已知,若证得AC⊥BC,则据面面垂直的性质定理即可.转化成在平面ABCD,能否有AC⊥BC,易证成立.
(Ⅱ)设AC∩BD=N,则面AMF∩平面BDF=FN,只需AM∥FN即可.而CN:NA=1:2.故应有
EM:FM=1:2
(Ⅰ)在梯形 中,
中,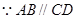 ,
,
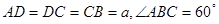
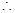 四边形
四边形 是等腰梯形,
是等腰梯形,
且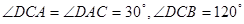
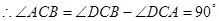
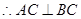
又 平面
平面 平面
平面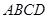 ,交线为
,交线为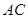 ,
,
 平面
平面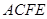
∴平面BCF⊥平面ACFE;
(Ⅱ)解法一、当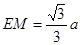 时,
时,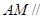 平面
平面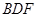 ,
,
在梯形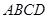 中,设
中,设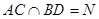 ,连接
,连接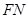 ,则
,则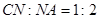
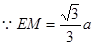 ,而
,而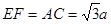
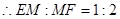 ,
,
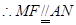 ,
,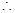 四边形
四边形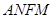 是平行四边形,
是平行四边形,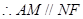
又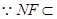 平面
平面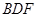 ,
,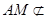 平面
平面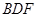
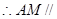 平面
平面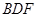
解法二:当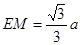 时,
时,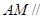 平面
平面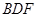 ,
,
由(Ⅰ)知,以点 为原点,
为原点,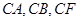 所在直线为坐标轴,建立空间直角坐标系,
所在直线为坐标轴,建立空间直角坐标系,
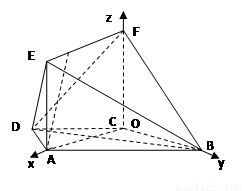
则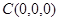 ,
,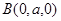 ,
,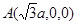 ,
,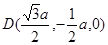 ,
,
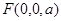 ,
,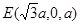
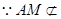 平面
平面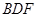 ,
,
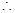
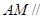 平面
平面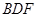
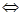
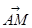 与
与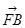 、
、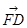 共面,
共面,
也等价于存在实数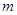 、
、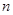 ,使
,使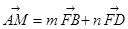 ,
,
设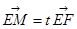 .
.
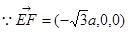 ,
,
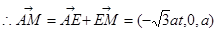
又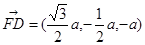 ,
,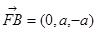 ,
,
从而要使得: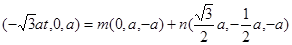 成立,
成立,
需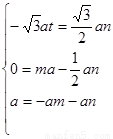 ,解得
,解得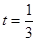
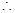 当
当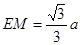 时,
时,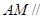 平面
平面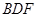

练习册系列答案
相关题目