题目内容
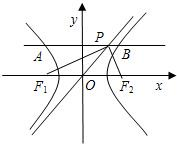 我们定义双曲线C:
我们定义双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
(1)求证:PF1⊥PF2;
(2)求证:PF1平分∠APO;
(3)你能否在未证明(1)下,直接证明(2)?请写下你的理由.
分析:(1)根据题意,分析“虚近点”的定义,联立由
得P的坐标,由向量数量积的公式,计算
•
,可得其结果为0,即可证PF1⊥PF2;
(2)由(1)知△F1PF2为直角三角形,且O为斜边F1F2的中点,由直角三角形的性质,可得∠OF1P=∠OPF1,进而可得∠OF1P=∠APF1,即可证PF1平分∠APO;
(3)由(1)可得P的坐标,可得|OP|=C,又由|OF1|=c,可得∠OF1P=∠OPF1,进而根据AB∥F1F2,得∠OF1P=∠APF1,即可得∠OPF1=∠APF1,即可证PF1平分∠APO.
|
| PF1 |
| PF2 |
(2)由(1)知△F1PF2为直角三角形,且O为斜边F1F2的中点,由直角三角形的性质,可得∠OF1P=∠OPF1,进而可得∠OF1P=∠APF1,即可证PF1平分∠APO;
(3)由(1)可得P的坐标,可得|OP|=C,又由|OF1|=c,可得∠OF1P=∠OPF1,进而根据AB∥F1F2,得∠OF1P=∠APF1,即可得∠OPF1=∠APF1,即可证PF1平分∠APO.
解答:证明:(1)双曲线C在第一、三象限的渐近线方程为y=
x,
由
得P(a,b),
∴
•
=(-c-a,-b)•(c-a,-b)=a2-c2+b2=0,
得PF1⊥PF2;
(2)由(1)知△F1PF2为直角三角形,且O为斜边F1F2的中点,
∴OP=OF1,有∠OF1P=∠OPF1,
又∵AB∥F1F2,得∠OF1P=∠APF1,
∴∠OPF1=∠APF1,
∴PF1平分∠APO,同理得证PF2平分∠BPO;
(3)能直接证明,证明如下:
同(1)的方法,可求得P(a,b),
∴|OP|=
=c,
又∵|OF1|=c,∴∠OF1P=∠OPF1,
又∵AB∥F1F2,得∠OF1P=∠APF1,∴∠OPF1=∠APF1,
∴PF1平分∠APO.
| b |
| a |
由
|
∴
| PF1 |
| PF2 |
得PF1⊥PF2;
(2)由(1)知△F1PF2为直角三角形,且O为斜边F1F2的中点,
∴OP=OF1,有∠OF1P=∠OPF1,
又∵AB∥F1F2,得∠OF1P=∠APF1,
∴∠OPF1=∠APF1,
∴PF1平分∠APO,同理得证PF2平分∠BPO;
(3)能直接证明,证明如下:
同(1)的方法,可求得P(a,b),
∴|OP|=
| a2+b2 |
又∵|OF1|=c,∴∠OF1P=∠OPF1,
又∵AB∥F1F2,得∠OF1P=∠APF1,∴∠OPF1=∠APF1,
∴PF1平分∠APO.
点评:本题考查双曲线的性质与应用,解题时,注意分析题意,把握好“虚近点”的定义,结合双曲线的定义与性质,从而解题.

练习册系列答案
相关题目
 (2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.
(2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.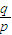 ,其中p、q均为整数且p、q互质)
,其中p、q均为整数且p、q互质)
 ,其中p、q均为整数且p、q互质)
,其中p、q均为整数且p、q互质)