题目内容
【题目】已知点A（1，0），若点B是曲线y=f（x）上的点，且线段AB的中点在曲线y=g（x）上，则称点B是函数y=f（x）关于函数g（x）的一个“关联点”，已知f（x）=|log2x|，g（x）=（ 
）x ， 则函数f（x）关于函数g（x）的“关联点”的个数是（ ）
A.1
B.2
C.3
D.4
【答案】B
【解析】解：令点B（x，|log2x|），x＞0， A，B的中点C（ 
， 
|log2x|）．
由于点C在函数g（x）=（ ）x的图象上，
故有 |log2x|=（ ） 
= 
（ ）x ，
即|log2x|= 
（ ）x ，
故函数f（x）关于函数g（x）的“关联点”的个数是，
即为函数y=|log2x|和曲线y= （ ）x的交点的个数．
在同一个坐标系中，画出函数y=|log2x|和y= （ ）x的 
的图象，
由图象知两个函数的交点个数为2个，
则函数f（x）关于函数g（x）的“关联点”的个数是2，
故故选：B．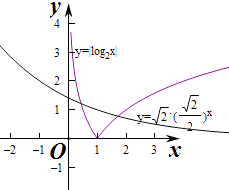
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
