题目内容
17.求事件A、B、C满足条件P(A)>0,B和C互斥试证明:P(BUC|A)=P(B|A)+P(C|A)分析 B与C互斥,可得AB与AC互斥,有P(AB∪AC)=P(AB)+P(AC),再利用条件概率,即可证明结论.
解答 证明:∵B与C互斥,∴AB与AC互斥,有P(AB∪AC)=P(AB)+P(AC),
∴P(B∪C|A)=$\frac{P[A(B∪C)]}{P(A)}$=$\frac{P(AB∪AC)}{P(A)}$=$\frac{P(AB)+P(AC)}{P(A)}$=$\frac{P(AB)}{P(A)}$+$\frac{P(AC)}{P(A)}$=P(B|A)+P(C|A).
点评 本题考查条件概率,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,给出下列两个命题:
,给出下列两个命题: ,方程
,方程 有解.
有解. 若
若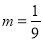 ,则
,则 .
. B.
B. C.
C.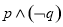 D.
D.
 如图,PA与圆O相切于A,不过圆心O的割线PCB与直径AE相交于D点.已知∠BPA=30°,AD=2,PC=1,则圆O的半径等于7.
如图,PA与圆O相切于A,不过圆心O的割线PCB与直径AE相交于D点.已知∠BPA=30°,AD=2,PC=1,则圆O的半径等于7.