题目内容
12.数列{an}中,a1=1,a2=3,an2-an-1•an+1=(-1)n-1(n≥2),那么a4=33.分析 直接由已知及数列递推式求得a4的值.
解答 解:由a1=1,a2=3,an2-an-1•an+1=(-1)n-1(n≥2),
得${{a}_{2}}^{2}-{a}_{1}{a}_{3}=-1$,
∴32-1×a3=-1,a3=10;
${{a}_{3}}^{2}-{a}_{2}{a}_{4}=1$,
∴102-3a4=1,a4=33.
故答案为:33.
点评 本题考查了数列递推式,考查了计算能力,是基础的计算题.

练习册系列答案
相关题目
20.过抛物线C1:y=ax2(a>0)的焦点作y轴的垂线交抛物线C1于A,B两点,若△OAB(O是坐标原点)是面积为$\frac{1}{2}$的等腰三角形,则a的值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
19.已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<2π)一个周期内的一系列对应值如表:
(1)求f(x)的解析式;
(2)求函数g(x)=f(x)+$\sqrt{3}$sin2x的单调递增区间.
| x | 0 | $\frac{π}{6}$ | $\frac{π}{4}$ | $\frac{π}{2}$ |
| y | 1 | $\frac{1}{2}$ | 0 | -1 |
(2)求函数g(x)=f(x)+$\sqrt{3}$sin2x的单调递增区间.
 与直线
与直线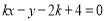 有两个相异的交点时,实数k的取值范围是( )
有两个相异的交点时,实数k的取值范围是( ) B.
B.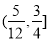 C.
C. D.
D.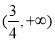
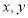 满足条件
满足条件 ,且
,且 的最小值为6,
的最小值为6, ,则
,则 ___________.
___________.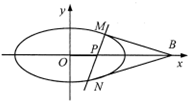 如图,已知椭圆C:$\frac{{x}^{2}}{4}$+y2=1,过点P(1,0)作斜率为k的直线l,且直线l与椭圆C交于两个不同的点M、N.
如图,已知椭圆C:$\frac{{x}^{2}}{4}$+y2=1,过点P(1,0)作斜率为k的直线l,且直线l与椭圆C交于两个不同的点M、N.