题目内容
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.(1)sin213°+cos217°-sin13°cos17°
(2)sin215°+cos215°-sin15°cos15°
(3)sin218°+cos212°-sin18°cos12°
(4)sin2(-18°)+cos248°-sin2(-18°)cos48°
(5)sin2(-25°)+cos255°-sin2(-25°)cos55°
(Ⅰ)试从上述五个式子中选择一个,求出这个常数
(Ⅱ)根据(Ⅰ)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
【答案】分析:(Ⅰ)选择(2),由sin215°+cos215°-sin15°cos15°=1- sin30°=
sin30°= ,可得这个常数的值.
,可得这个常数的值.
(Ⅱ)推广,得到三角恒等式sin2α+cos2(30°-α)-sinαcos(30°-α)= .证明方法一:直接利用两角差的余弦公式代入等式的左边,化简可得结果.
.证明方法一:直接利用两角差的余弦公式代入等式的左边,化简可得结果.
证明方法二:利用半角公式及两角差的余弦公式把要求的式子化为 +
+ -sinα(cos30°cosα+sin30°sinα),即 1-
-sinα(cos30°cosα+sin30°sinα),即 1- +
+ cos2α+
cos2α+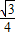 sin2α
sin2α
- sin2α-
sin2α-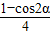 ,化简可得结果.
,化简可得结果.
解答:解:选择(2),计算如下:
sin215°+cos215°-sin15°cos15°=1- sin30°=
sin30°= ,故 这个常数为
,故 这个常数为 .
.
(Ⅱ)根据(Ⅰ)的计算结果,将该同学的发现推广,得到三角恒等式sin2α+cos2(30°-α)-sinαcos(30°-α)= .
.
证明:(方法一)sin2α+cos2(30°-α)-sinαcos(30°-α)=sin2α+ -sinα(cos30°cosα+sin30°sinα)
-sinα(cos30°cosα+sin30°sinα)
=sin2α+ cos2α+
cos2α+ sin2α+
sin2α+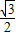 sinαcosα-
sinαcosα-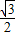 sinαcosα-
sinαcosα- sin2α=
sin2α= sin2α+
sin2α+ cos2α=
cos2α= .
.
(方法二)sin2α+cos2(30°-α)-sinαcos(30°-α)=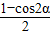 +
+ -sinα(cos30°cosα+sin30°sinα)
-sinα(cos30°cosα+sin30°sinα)
=1-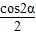 +
+ (cos60°cos2α+sin60°sin2α)-
(cos60°cos2α+sin60°sin2α)- sin2α-
sin2α- sin2α
sin2α
=1- +
+ cos2α+
cos2α+ sin2α-
sin2α- sin2α-
sin2α- =1-
=1- -
- +
+ =
= .
.
点评:本题主要考查两角差的余弦公式,二倍角公式及半角公式的应用,考查归纳推理以及计算能力,属于中档题.
 sin30°=
sin30°= ,可得这个常数的值.
,可得这个常数的值.(Ⅱ)推广,得到三角恒等式sin2α+cos2(30°-α)-sinαcos(30°-α)=
 .证明方法一:直接利用两角差的余弦公式代入等式的左边,化简可得结果.
.证明方法一:直接利用两角差的余弦公式代入等式的左边,化简可得结果.证明方法二:利用半角公式及两角差的余弦公式把要求的式子化为
 +
+ -sinα(cos30°cosα+sin30°sinα),即 1-
-sinα(cos30°cosα+sin30°sinα),即 1- +
+ cos2α+
cos2α+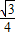 sin2α
sin2α-
 sin2α-
sin2α-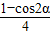 ,化简可得结果.
,化简可得结果.解答:解:选择(2),计算如下:
sin215°+cos215°-sin15°cos15°=1-
 sin30°=
sin30°= ,故 这个常数为
,故 这个常数为 .
.(Ⅱ)根据(Ⅰ)的计算结果,将该同学的发现推广,得到三角恒等式sin2α+cos2(30°-α)-sinαcos(30°-α)=
 .
.证明:(方法一)sin2α+cos2(30°-α)-sinαcos(30°-α)=sin2α+
 -sinα(cos30°cosα+sin30°sinα)
-sinα(cos30°cosα+sin30°sinα)=sin2α+
 cos2α+
cos2α+ sin2α+
sin2α+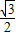 sinαcosα-
sinαcosα-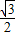 sinαcosα-
sinαcosα- sin2α=
sin2α= sin2α+
sin2α+ cos2α=
cos2α= .
.(方法二)sin2α+cos2(30°-α)-sinαcos(30°-α)=
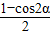 +
+ -sinα(cos30°cosα+sin30°sinα)
-sinα(cos30°cosα+sin30°sinα)=1-
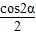 +
+ (cos60°cos2α+sin60°sin2α)-
(cos60°cos2α+sin60°sin2α)- sin2α-
sin2α- sin2α
sin2α=1-
 +
+ cos2α+
cos2α+ sin2α-
sin2α- sin2α-
sin2α- =1-
=1- -
- +
+ =
= .
.点评:本题主要考查两角差的余弦公式,二倍角公式及半角公式的应用,考查归纳推理以及计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. ;
; ;
; ;
; ;
; .
.