题目内容
已知函数f(x)=ax+3在区间[0,2]上有零点,则实数a的取值范围是________.
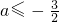
分析:f(x)是单调函数,在[-2,3]上存在零点,应有f(0)f(2)≤0,解不等式求出数m的取值范围.
解答:由题意知a≠0,∴f(x)是单调函数,
又在闭区间[0,2]上存在零点,
∴f(0)f(2)≤0,
即3(2a+3)≤0,解得
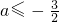 .
.故答案为:
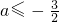 .
.点评:本题考查函数的单调性、单调区间,及函数存在零点的条件.解答的关键是根据题意转化成:f(0)f(2)≤0.属基础题.

练习册系列答案
相关题目