题目内容
直线l经过点(3,2),且在两坐标轴上的截距相等,求直线l的方程.
2x-3y=0或x+y-5=0.
解法1:(借助点斜式求解)
由于直线l在两轴上有截距,因此直线不与x、y轴垂直,斜率存在,且k≠0.设直线方程为y-2=k(x-3),令x=0,则y=-3k+2;令y=0,则x=3-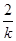 .
.
由题设可得-3k+2=3-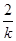 ,解得k=-1或k=
,解得k=-1或k=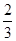 .
.
故l的方程为y-2=-(x-3)或y-2=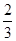 (x-3).
(x-3).
即直线l的方程为x+y-5=0或2x-3y=0.
解法2:(利用截距式求解)由题设,设直线l在x、y轴的截距均为a.
若a=0,则l过点(0,0).又过点(3,2),∴l的方程为y=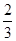 x,即l:2x-3y=0.
x,即l:2x-3y=0.
若a≠0,则设l为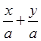 =1.由l过点(3,2),知
=1.由l过点(3,2),知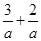 =1,故a=5.
=1,故a=5.
∴l的方程为x+y-5=0.
综上可知,直线l的方程为2x-3y=0或x+y-5=0.
由于直线l在两轴上有截距,因此直线不与x、y轴垂直,斜率存在,且k≠0.设直线方程为y-2=k(x-3),令x=0,则y=-3k+2;令y=0,则x=3-
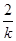 .
.由题设可得-3k+2=3-
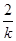 ,解得k=-1或k=
,解得k=-1或k=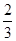 .
.故l的方程为y-2=-(x-3)或y-2=
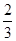 (x-3).
(x-3).即直线l的方程为x+y-5=0或2x-3y=0.
解法2:(利用截距式求解)由题设,设直线l在x、y轴的截距均为a.
若a=0,则l过点(0,0).又过点(3,2),∴l的方程为y=
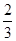 x,即l:2x-3y=0.
x,即l:2x-3y=0.若a≠0,则设l为
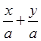 =1.由l过点(3,2),知
=1.由l过点(3,2),知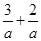 =1,故a=5.
=1,故a=5.∴l的方程为x+y-5=0.
综上可知,直线l的方程为2x-3y=0或x+y-5=0.

练习册系列答案
相关题目
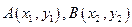 分别在直线l1:x+y-7=0和l2:x+y-5=0上移动,则AB中点M到原点距离的最小值为( ).
分别在直线l1:x+y-7=0和l2:x+y-5=0上移动,则AB中点M到原点距离的最小值为( ).



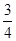 (x-2),则该直线另外三种特殊形式的方程为______________,______________,______________.
(x-2),则该直线另外三种特殊形式的方程为______________,______________,______________.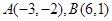 ,点
,点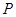 在
在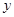 轴上,且
轴上,且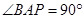 ,则点
,则点