题目内容
设m，n∈R，若直线l：mx＋ny－1＝0与x轴相交于点A，与y轴相交于点B，且l与圆x2＋y2＝4相交所得弦的长为2，O为坐标原点，则△AOB面积的最小值为________．
3
解析
练习册系列答案
阅读快车系列答案
相关题目
，若分别以
为弦作两外切的圆
和圆
，且两圆半径相等，则圆的半径为 ．
与圆
的位置关系是 （填相交、相切、相离）
和
将单位圆
分成长度相等的四段弧，则
.
的半径为1，圆心在第一象限，且与直线
和
轴相切，则该圆的标准方程是________.圆心在
轴上，且过点
的圆的方程为（ ）
A． | B． |
C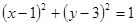． | D． |
题目内容
设m，n∈R，若直线l：mx＋ny－1＝0与x轴相交于点A，与y轴相交于点B，且l与圆x2＋y2＝4相交所得弦的长为2，O为坐标原点，则△AOB面积的最小值为________．
3
解析
阅读快车系列答案圆心在轴上，且过点的圆的方程为（ ）
| A． | B． |
| C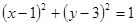． | D． |
的最小值为________．