题目内容

已知数据x₁，x₂，x₃，…，x₁₀的平均数为6，标准差为 $数学公式$ ，则数据x₁，x₂，…，x₅的平均数的取值范围是________．

$\text{[math]}$
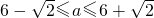
分析：法一：设x₁，x₂，…，x₅的平均数为a，x₆，x₇，…，x₁₀的平均数为b，则b=12-a，利用条件：“数据x₁，x₂，x₃，…，x₁₀的平均数为6，标准差为 $\text{[math]}$ ，”得出关于a的不等关系，最后解一个二次不等式即可；
法二：（运用柯西不等式）设x₁，x₂，…，x₅的平均数为a，x₆，x₇，…，x₁₀的平均数为b，则b=12-a，利用柯西不等式得出：x₁²+x₂²+…+x₁₀²≥5a²+5（12-a）²，解之即可．
解答：由（x₁-6）²+（x₂-6）²+…+（x₁₀-6）²=20，
得：x₁²+x₂²+…+x₁₀²-12（x₁+x₂+…+x₁₀）+360=20
即 x₁²+x₂²+…+x₁₀²=380
设x₁，x₂，…，x₅的平均数为a，x₆，x₇，…，x₁₀的平均数为b，则b=12-a
结合方差定义（x₁-a）²+（x₂-a）²+…+（x₅-a）²≥0
展开得：x₁²+x₂²+…+x₅²-2a（x₁+x₂+…+x₅）+5a²≥0
即 x₁²+x₂²+…+x₅²-2a•5a+5a²≥0，x₁²+x₂²+…+x₅²≥5a²，
同理x₆²+x₇²+…+x₁₀²≥5b²=5（12-a）²
得：x₁²+x₂²+…+x₁₀²≥5a²+5（12-a）²，即 380≥5a²+5（12-a）²a²-12a+34≤0得 $\text{[math]}$
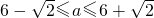
另解：（运用柯西不等式）
设x₁，x₂，…，x₅的平均数为a，x₆，x₇，…，x₁₀的平均数为b，则b=12-a
由 $\text{[math]}$ ， $\text{[math]}$
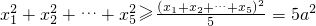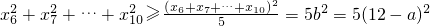
得：x₁²+x₂²+…+x₁₀²≥5a²+5（12-a）²，即 380≥5a²+5（12-a）²a²-12a+34≤0得 $\text{[math]}$
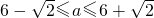
点评：本小题主要考查极差、方差与标准差、柯西不等式、不等式的解法等基础知识，考查运算求解能力，考查化归与转化思想．属于基础题．