题目内容
【题目】某地要建造一个边长为2（单位：km）的正方形市民休闲公园OABC，将其中的区域ODC开挖成一个池塘，如图建立平面直角坐标系后，点D的坐标为（1，2），曲线OD是函数y=ax2图象的一部分，对边OA上一点M在区域OABD内作一次函数y=kx+b（k＞0）的图象，与线段DB交于点N（点N不与点D重合），且线段MN与曲线OD有且只有一个公共点P，四边形MABN为绿化风景区：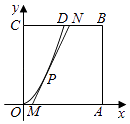 
（1）求证：b=﹣ 
；
（2）设点P的横坐标为t，①用t表示M、N两点坐标；②将四边形MABN的面积S表示成关于t的函数S=S（t），并求S的最大值．
【答案】
（1）证明：函数y=ax2过点D（1，2），
代入计算得a=2，
∴y=2x2；
由 
，消去y得2x2﹣kx﹣b=0，
由线段MN与曲线OD有且只有一个公共点P，
得△=（﹣k）2﹣4×2×b=0，
解得b=﹣ 
（2）解：设点P的横坐标为t，则P（t，2t2）；
①直线MN的方程为y=kx+b，
即y=kx﹣ 过点P，
∴kt﹣ =2t2，
解得k=4t；
y=4tx﹣2t2
令y=0，解得x= 
，∴M（ ，0）；
令y=2，解得x= + 
，∴N（ + ，2）；
②将四边形MABN的面积S表示成关于t的函数为
S=S（t）=2×2﹣ 
×2×[ +（ + ）]=4﹣（t+ ）；
由t+ ≥2 
= 
，当且仅当t= ，即t= 
时“=”成立，
所以S≤4﹣2 ；即S的最大值是4﹣
【解析】（1）根据函数y=ax2过点D，求出解析式y=2x2；由 ，消去y得△=0即可证明b=﹣ ；（2）写出点P的坐标（t，2t2），代入①直线MN的方程，用t表示出直线方程为y=4tx﹣2t2 ， 令y=0，求出M的坐标；令y=2求出N的坐标； ②将四边形MABN的面积S表示成关于t的函数S（t），利用基本不等式求出S的最大值．
