题目内容
已知:函数![]() (
(![]() 是常数)是奇函数,且满足
是常数)是奇函数,且满足![]() ,
,
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)试判断函数![]() 在区间
在区间![]() 上的单调性并说明理由;
上的单调性并说明理由;
(Ⅲ)试求函数![]() 在区间
在区间![]() 上的最小值.
上的最小值.![]()
(Ⅰ)![]() ,
,![]() .
.
(Ⅱ)函数![]() 在区间
在区间![]() 上为减函数.
上为减函数.
(Ⅲ)![]() 是函数的最小值点,即函数
是函数的最小值点,即函数![]() 在
在![]() 取得最小值
取得最小值![]() .
.
解析:
(Ⅰ)∵函数![]() 是奇函数,则
是奇函数,则![]()
即 ![]() ∴
∴![]() …………………………2分
…………………………2分
由![]() 得
得![]() 解得
解得![]()
∴![]() ,
,![]() . …………………………5分
. …………………………5分
(Ⅱ)由(Ⅰ)知![]() , ∴
, ∴![]() , ………………6分
, ………………6分
当![]() 时
时![]() ,
,![]() …………………………8分
…………………………8分
∴![]() ,即函数
,即函数![]() 在区间
在区间![]() 上为减函数. …………………………9分
上为减函数. …………………………9分
(Ⅲ)由![]() =0,
=0,![]() 得
得![]() …………………………11分
…………………………11分
∵当![]() ,
,![]() ,∴
,∴![]() ,
,
即函数![]() 在区间
在区间![]() 上为增函数 …………………………13分
上为增函数 …………………………13分
∴![]() 是函数的最小值点,即函数
是函数的最小值点,即函数![]() 在
在![]() 取得最小值
取得最小值![]() . ………14分
. ………14分

练习册系列答案
相关题目
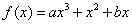 (其中常数
(其中常数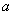 、
、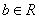 ),
),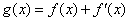 是奇函数。
是奇函数。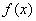 的表达式;
的表达式;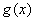 的单调性。
的单调性。