题目内容
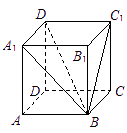在正方体ABCD－A1B1C1D1中，直线A1B与平面BC1D1所
成角的正切值为 （ ）
A．
B．
C．1 D．
Ｂ
解析:
先作出直线A1B与平面BC1D1所成角，再通过解三角形求出其正切值．如图，连结
交
于
，连结
．由
，
，又
，得
，所以
就是直线A1B与平面BC1D1所成角．在直角
中，求得
，故选Ｂ．
评析：平面的斜线与平面所成的角，就是这条斜线与它在该
平面上的射影所成的锐角，根据题目的条件作出斜线在该平
面上的射影是实现解题的关键，而作射影的关键则是作出平
面的垂线，要注意面面垂直的性质在作平面的垂线时的应用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在正方体ABCD-A1B1C1D1中，E是棱A1B1的中点，则A1B与D1E所成角的余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在正方体ABCD-A1B1C1D1中，AB与平面A1BC1所成角的正弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
（本小题满分12分）
在正方体ABCD－A′B′C′D′中，点M是棱AA′的中点，点O是对角线BD′的中点.
（Ⅰ）求证：OM为异面直线AA′和BD′的公垂线；
（Ⅱ）求二面角M－BC′－B′的大小；
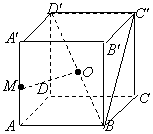
（Ⅰ）求证：OM为异面直线AA′和BD′的公垂线；
（Ⅰ）求证：OM为异面直线AA′和BD′的公垂线；