题目内容
在正方体ABCD-A′B′C′D′中,点M是棱AA′的中点,点O是对角线BD′的中点.

 (Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅱ)求二面角M-BC′-B′的大小;
 |
解法一:(1)连结AC,取AC中点K,则K为BD的中点,连结OK
能力和逻辑推理能力,考查应用向量知识解决数学问题的能力。
本小题主要考查异面直线、直线与平面垂直、二面角、正方体等基础知识,并考查空间想象
因为M是棱AA’的中点,点O是BD’的中点
所以AM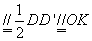
 所以MO
所以MO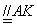
由AA’⊥AK,得MO⊥AA’
因为AK⊥BD,AK⊥BB’,所以AK⊥平面BDD’B’
所以AK⊥BD’
所以MO⊥BD’
又因为OM是异面直线AA’和BD’都相交
故OM为异面直线AA'和BD'的公垂线…………6分
(2)取BB’中点N,连结MN,则MN⊥平面BCC’B’
过点N作NH⊥BC’于H,连结MH
则由三垂线定理得BC’⊥MH
从而,∠MHN为二面角M-BC’-B’的平面角
MN=1,NH=Bnsin45°=
在Rt△MNH中,tan∠MHN=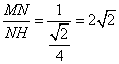
故二面角M-BC’-B’的大小为arctan2 …………………………………………12分
…………………………………………12分
解法二:
以点D为坐标原点,建立如图所示空间直角坐标系D-xyz
则A(1,0,0),B(1,1,0),C(0,1,0),A’(1,0,1),C’(0,1,1),D’(0,0,1)
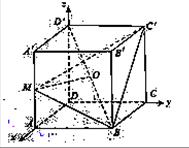 (1)因为点M是棱AA’的中点,点O是BD’的中点
(1)因为点M是棱AA’的中点,点O是BD’的中点
所以M(1,0, 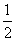 ),O(
),O(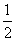 ,
,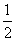 ,
,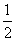 )
)
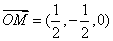 ,
, =(0,0,1),
=(0,0,1),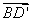 =(-1,-1,1)
=(-1,-1,1)
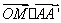 =0,
=0, 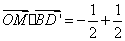 +0=0
+0=0
所以OM⊥AA’,OM⊥BD’
又因为OM与异面直线AA’和BD’都相交
故OM为异面直线AA'和BD'的公垂线.………………………………6分
(2)设平面BMC'的一个法向量为 =(x,y,z)
=(x,y,z)
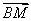 =(0,-1,
=(0,-1,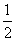 ),
),
 =(-1,0,1)
=(-1,0,1)
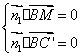 即
即
取z=2,则x=2,y=1,从而 =(2,1,2)
=(2,1,2)
取平面BC'B'的一个法向量为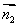 =(0,1,0)
=(0,1,0)
cos
由图可知,二面角M-BC'-B'的平面角为锐角
故二面角M-BC'-B'的大小为arccos ………………………………………………12分
………………………………………………12分
(19)
(Ⅰ)1证明两角和的余弦公式 ;
;
2由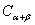 推导两角和的正弦公式
推导两角和的正弦公式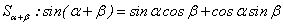 .
.
(Ⅱ)已知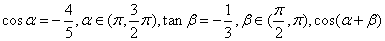 ,求
,求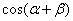
解:(1)①如图,在执教坐标系xOy内做单位圆O,并作出角α、β与-β,使角α的始边为
Ox,交⊙O于点P1,终边交⊙O于P2;角β的始边为OP2,终边交⊙O于P3;角-β的始边为OP1,终边交⊙O于P4.
则P1(1,0),P2(cosα,sinα)
P3(cos(α+β),sin(α+β)),P4(cos(-β),sin(-β))
由P1P3=P2P4及两点间的距离公式,得
[cos(α+β)-1]2+sin2(α+β)=[cos(-β)-cosα]2+[sin(-β)-sinα]2
展开并整理得: cos(α+β)= (cosαcosβ-sinαsinβ)
∴cos(α+β)=cosαcosβ-sinαsinβ.……………………4分
②由①易得cos(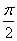 -α)=sinα,sin(
-α)=sinα,sin(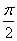 -α)=cosα
-α)=cosα
sin(α+β)=cos[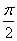 -(α+β)]=cos[(
-(α+β)]=cos[(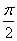 -α)+(-β)]
-α)+(-β)]
=cos(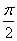 -α)cos(-β)-sin(
-α)cos(-β)-sin(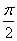 -α)sin(-β)
-α)sin(-β)
=sinαcosβ+cosαsinβ……………………………………6分
(2)∵α∈(π,),cosα=-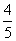
∴sinα=-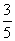
∵β∈(,π),tanβ=-
∴cosβ=-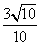 ,sinβ=
,sinβ=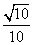
cos(α+β)=cosαcosβ-sinαsinβ
=(-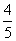 )×(-
)×(-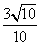 )-(-
)-(-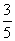 )×
)×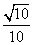
=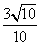

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|

 (Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;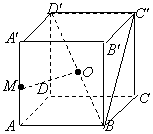
 (Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;