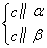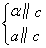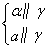题目内容
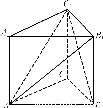
如图，直三棱柱ABC－A1B1C1中，D、E分别是棱BC、AB的中点，点F在棱CC1上，已知AB＝AC，AA1＝3，BC＝CF＝2.
(1)求证：C1E∥平面ADF；
(2)设点M在棱BB1上，当BM为何值时，平面CAM⊥平面ADF?
（1）见解析（2）当BM＝1时
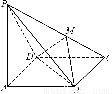
【解析】(1)证明：连结CE交AD于O，连结OF.
因为CE，AD为△ABC中线，所以O为△ABC的重心，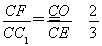
.
从而OF//C1E.OF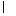
平面ADF，C1E
平面ADF，所以C1E∥平面ADF.
(2)【解析】
当BM＝1时，平面CAM⊥平面ADF.
在直三棱柱ABC－A1B1C1中，由于B1B⊥平面ABC，BB1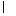平面B1BCC1，所以平面B1BCC1⊥平面ABC.由于AB＝AC，D是BC中点，所以AD⊥BC.又平面B1BCC1∩平面ABC＝BC,所以AD⊥平面B1BCC1.而CM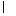平面B1BCC1，于是AD⊥CM.因为BM＝CD＝1，BC＝CF＝2，所以Rt△CBM≌Rt△FCD，所以CM⊥DF.DF与AD相交，所以CM⊥平面ADF.CM⊥平面CAM，所以平面CAM⊥平面ADF.当BM＝1时，平面CAM⊥平面ADF.
练习册系列答案
金博士一点全通系列答案
相关题目
