题目内容
【题目】设![]() 是各项均为正数的等差数列,
是各项均为正数的等差数列,![]() ,
,![]() 是
是![]() 和
和![]() 的等比中项,
的等比中项,![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() .
.
(1)求![]() 和
和![]() 的通项公式;
的通项公式;
(2)设数列![]() 的通项公式
的通项公式 .
.
(i)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(ii)求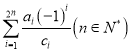 .
.
【答案】(1)![]() ,
,![]() ;(2)(i)
;(2)(i)![]() ;(ii)
;(ii)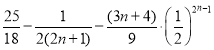
【解析】
(1)因为![]() ,
,![]() 是
是![]() 和
和![]() 的等比中项,根据等比中项可求得
的等比中项,根据等比中项可求得![]() ,再根据等差数列的通项公式求出
,再根据等差数列的通项公式求出![]() ,利用
,利用![]() 与
与![]() 的关系,证出
的关系,证出![]() 是以2为首项,2为公比的等比数列,再利用等比数列的通项公式求出
是以2为首项,2为公比的等比数列,再利用等比数列的通项公式求出![]() 的通项公式;
的通项公式;
(2)![]() 根据(1)中
根据(1)中![]() 和
和![]() 的通项公式,列出数列
的通项公式,列出数列![]() 的通项公式,利用分组求和法,分成奇数组和偶数组,即可求出数列
的通项公式,利用分组求和法,分成奇数组和偶数组,即可求出数列![]() 的前
的前![]() 项和
项和![]() ;
;
![]() 将
将![]() 分为奇数和偶数两种情况,当
分为奇数和偶数两种情况,当![]() 为奇数时,设
为奇数时,设![]() ,运用裂项相消法化简求出结果;当
,运用裂项相消法化简求出结果;当![]() 为偶数时,设
为偶数时,设![]() ,运用错位相减法求出结果;分别求解出后,相加求得
,运用错位相减法求出结果;分别求解出后,相加求得![]() 的值即可.
的值即可.
(1)解:设等差数列![]() 的公差为
的公差为![]() ,
,
因为![]() ,
,![]() 是
是![]() 和
和![]() 的等比中项,
的等比中项,
所以![]() ,即
,即![]() ,
,
解得![]() ,因为
,因为![]() 是各项均为正数的等差数列,
是各项均为正数的等差数列,
所以![]() ,
,
故![]() ,
,
因为![]() ,所以
,所以![]() ,
,
两式相减得:![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
![]() 是以2为首项,2为公比的等比数列,
是以2为首项,2为公比的等比数列,
![]() .
.
(2)(i)解: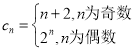 ,
,
所以![]()
![]() .
.
(ii)解:当![]() 为奇数时,
为奇数时,
设![]()
![]() ,
,
当![]() 为偶数时,
为偶数时,
设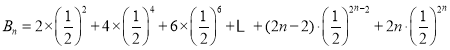 ,
,
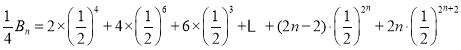 ,
,
所以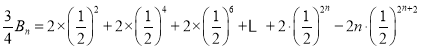 ,
,
故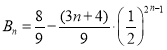 ,
,
所以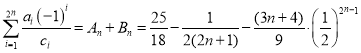 .
.

练习册系列答案
相关题目