题目内容
12.已知m∈R,函数f(x)=$\left\{\begin{array}{l}{|2x+1|,x<1}\\{lo{g}_{2}(x-1),x>1}\end{array}\right.$,g(x)=x2-2x+2m-1,若函数y=f(g(x))-m有6个零点,则实数m的取值范围是(0,$\frac{3}{5}$).分析 令g(x)=t,由题意画出函数y=f(t)的图象,利用y=f(t)与y=m的图象最多有3个零点,可知要使函数y=f(g(x))-m有6个零点,则t=x2-2x+2m-1中每一个t的值对应2个x的值,则t的值不能取最小值,求出y=f(t)与y=m交点横坐标的最小值,由其绝对值大于2m-2,结合0<m<3求得实数m的取值范围.
解答 解:函数f(x)=$\left\{\begin{array}{l}{|2x+1|,x<1}\\{lo{g}_{2}(x-1),x>1}\end{array}\right.$的图象如图所示,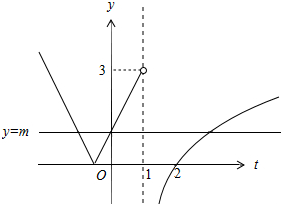
令g(x)=t,y=f(t)与y=m的图象最多有3个零点,
当有3个零点,则0<m<3,从左到右交点的横坐标依次t1<t2<t3,
由于函数y=f(g(x))-m有6个零点,t=x2-2x+2m-1,
则每一个t的值对应2个x的值,则t的值不能取最小值,
函数t=x2-2x+2m-1对称轴x=1,则t的最小值为1-2+2m-1=2m-2,
由图可知,2t1+1=-m,则${t}_{1}=\frac{-m-1}{2}$,
由于t1是交点横坐标中最小的,满足$\frac{-m-1}{2}>2m-2$①,
又0<m<3②,
联立①②得0$<m<\frac{3}{5}$.
∴实数m的取值范围是(0,$\frac{3}{5}$).
故答案为:(0,$\frac{3}{5}$).
点评 本题考查根的存在性及根的个数判断,考查数形结合的解题思想方法和数学转化思想方法,属有一定难度题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.若A={x|x∈N|x<2},可用列举法将集合{(x,y)|x∈A,y∈A}表示为( )
| A. | {(0,1)} | B. | {0,1} | C. | {(1,1),(1,2),(2,1),(2,2)} | D. | {(0,0),(0,1),(1,0),(1,1)} |
2.在区间(-$\frac{π}{2}$,$\frac{π}{2}$)上随机地取一个实数x,则事件“tanx≥$\frac{\sqrt{3}}{3}$”发生的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |