题目内容
18.(1)已知幂函数f(x)=(t3-t+1)x${\;}^{\frac{1}{5}(7+3t-2{t}^{2})}$ (t∈Z)是偶函数,且在区间[0,+∞)上是增函数,求整数t的值,并作出相应的幂函数的大致图象;(2)已知幂函数f(x)=$\frac{1}{{x}^{2-m-{m}^{2}}}$在(-∞,0)上是减函数.求m的最大负整数值.
分析 (1)由幂函数的定义、奇偶性和单调性,能求出整数t的值,并作出相应的幂函数的大致图象.
(2)由已知条件利用幂函数的性质得$\left\{\begin{array}{l}{{m}^{2}+m-2是偶数}\\{{m}^{2}+m-2>0}\end{array}\right.$,由此能求出m的最大负整数值.
解答 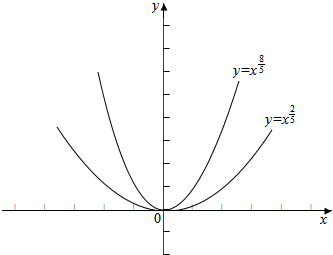 解:(1)∵幂函数f(x)=(t3-t+1)x${\;}^{\frac{1}{5}(7+3t-2{t}^{2})}$ (t∈z)是偶函数,
解:(1)∵幂函数f(x)=(t3-t+1)x${\;}^{\frac{1}{5}(7+3t-2{t}^{2})}$ (t∈z)是偶函数,
且在区间[0,+∞)上是增函数,
∴$\left\{\begin{array}{l}{{t}^{3}-t+1=1}\\{\frac{1}{5}(7+3t-2{t}^{2})>0}\\{7+3t-2{t}^{2}偶数}\end{array}\right.$,
解得t=1或t=-1.
t=1时,f(x)=${x}^{\frac{2}{5}}$,t=-1时,f(x)=${x}^{\frac{8}{5}}$.
(2)∵幂函数f(x)=$\frac{1}{{x}^{2-m-{m}^{2}}}$=${x}^{{m}^{2}+m-2}$在(-∞,0)上是减函数,
∴$\left\{\begin{array}{l}{{m}^{2}+m-2是偶数}\\{{m}^{2}+m-2>0}\end{array}\right.$,
解得m>1或m<-2,
∴m的最大负整数值为-3.
点评 本题主要考查幂函数的定义以及幂函数的性质,要求熟练掌握幂函数的定义和幂函数的性质,是基础题.

练习册系列答案
相关题目
10.1+4+7+10+…+(3n+4)+(3n+7)等于( )
| A. | $\frac{n(3n+8)}{2}$ | B. | $\frac{(n+2)(3n+8)}{2}$ | C. | $\frac{(n+3)(3n+8)}{2}$ | D. | $\frac{n(3n-1)}{2}$ |