题目内容
设常数a使方程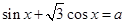
在闭区间[0,2
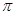]上恰有三个解
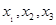，则
.
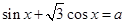在闭区间[0,2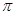]上恰有三个解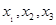，则 . 
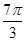
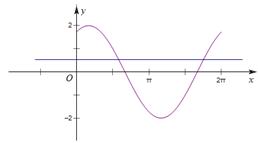
原方程可变为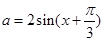
，如图作出函数
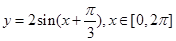的图象，再作直线
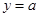，从图象可知函数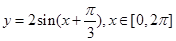在
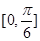上递增，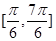
上递减，在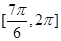
上递增，只有当
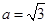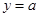时，直线与函数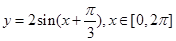的图象有三个交点，
，
，
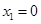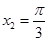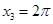，所以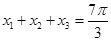
．
【考点】解三角方程，方程的解与函数图象的交点．
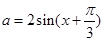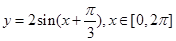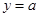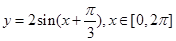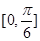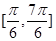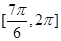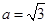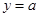，如图作出函数的图象，再作直线，从图象可知函数在上递增，上递减，在上递增，只有当时，直线与函数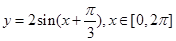的图象有三个交点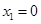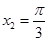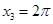，，，，所以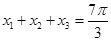．【考点】解三角方程，方程的解与函数图象的交点．
练习册系列答案
相关题目
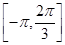上的函数y＝f(x)的图象关于直线x＝－
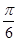对称，当x∈
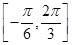时，函数f(x)＝Asin(ωx＋φ)
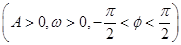的图象如图所示．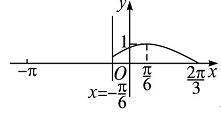
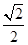的解．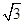
(sin2x－cos2x)－2sinxcosx.
，
.
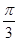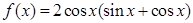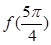的值；
的最小正周期及单调递增区间.
，
．
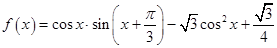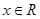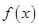的最小正周期；
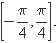上的最大值和最小值． 
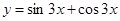的图象，可以将函数
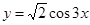的图象（ ）
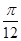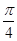个单位长
个单位长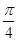
)(ω>0)的最小正周期为π．
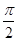]上的单调性．
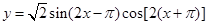是（ ）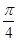 
的奇函数 B 周期为
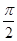的奇函数 D 周期为
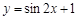的最小正周期为 ．