题目内容
空间点到平面的距离如下定义:过空间一点作平面的垂线,该点和垂足之间的距离即为该点到平面的距离.已知平面α,β,γ两两互相垂直,点A∈α,点A到β,γ的距离都是3,点P是α上的动点,满足p到β的距离是到p到点A距离的2倍,则点P的轨迹上的点到γ的距离的最小值为( )
A.
| B.3-2
| C.6-
| D.3-
|
设P(x,y),
P的轨迹方程为x=2
,
x2=4(x-3)2+4(y-3)2,
(y-3)2=
[x2-4(x-3)2]-
x2+6x-9,
当x=4时,最大值为3
∵(y-3)2=3,∴y=3+
,或y=3-
∴点P 的轨迹上的点到γ 的距离的最小值是3-
.
故选D.
P的轨迹方程为x=2
| (x-3)2+(y-3)2 |
x2=4(x-3)2+4(y-3)2,
(y-3)2=
| 1 |
| 4 |
| 3 |
| 4 |
当x=4时,最大值为3
∵(y-3)2=3,∴y=3+
| 3 |
| 3 |
∴点P 的轨迹上的点到γ 的距离的最小值是3-
| 3 |
故选D.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
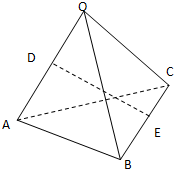 如图,空间四边形OABC各边以及AC,BO的边长都为a,点D,E分别是边OA,BC的中点,连接DE
如图,空间四边形OABC各边以及AC,BO的边长都为a,点D,E分别是边OA,BC的中点,连接DE 
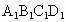 的棱长为1,E是
的棱长为1,E是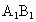 的中点,则下列五个命题:
的中点,则下列五个命题:
 的距离是
的距离是 ;
;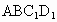 所成的角等于45°;
所成的角等于45°; 在正方体六个面内的射影围成的图形中,面积最小值为
在正方体六个面内的射影围成的图形中,面积最小值为 ;
;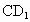 所成的角为
所成的角为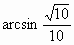 ;
;
 的大小为
的大小为

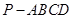 中,底面
中,底面 是矩形,
是矩形, 平面
平面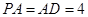 ,
, .
. 于点
于点 ,
, 是
是 中点.
中点.
 ⊥平面
⊥平面 ;
;  与平面
与平面 所成的角的正弦值;
所成的角的正弦值;