题目内容
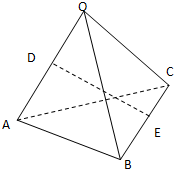 如图,空间四边形OABC各边以及AC,BO的边长都为a,点D,E分别是边OA,BC的中点,连接DE
如图,空间四边形OABC各边以及AC,BO的边长都为a,点D,E分别是边OA,BC的中点,连接DE (1)计算DE的长;
(2)求A点到平面OBC的距离.
分析:(1)连接AE,OE,由题设知OE=AE=
a,所以△OEA是等腰三角形.DE⊥AO,由此能求出DE的长.
(2)由AE⊥BC,OE⊥BC,知面ABC⊥面AOE.在面AOE中,作OF⊥AE,则OF⊥面ABC,所以,OF的长即为点O到面ABC的距离.由△AOE是等腰三角形,DE是底AO上的高,OF是AE边上的高,由面积公式得:
AO×DE=
AE×OF,由此能求出点O到平面ABC的距离.
| ||
| 2 |
(2)由AE⊥BC,OE⊥BC,知面ABC⊥面AOE.在面AOE中,作OF⊥AE,则OF⊥面ABC,所以,OF的长即为点O到面ABC的距离.由△AOE是等腰三角形,DE是底AO上的高,OF是AE边上的高,由面积公式得:
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)连接AE,OE,因空间四边形OABC各边以及AC,BO的长都是a,
D,E是OA,BC的中点,所以,OE=AE=
a,
所以△是等腰三角形.
所以DE⊥AO,
因此,DE=
=
=
a.
(2)∵AE⊥BC,OE⊥BC,
∴BC⊥面AOE,∴面ABC⊥面AOE.
在面AOE中,作OF⊥AE,则OF⊥面ABC,
所以,OF的长即为点O到面ABC的距离.
∵△AOE是等腰三角形,DE是底AO上的高,OF是AE边上的高,
∴由面积公式得:
AO×DE=
AE×OF,
即
×a×
a=
×
× OFa,
解得.OF=
a,所以点O到平面ABC的距离是
a.
D,E是OA,BC的中点,所以,OE=AE=
| ||
| 2 |
所以△是等腰三角形.
所以DE⊥AO,
因此,DE=
| OE2-OD2 |
|
| ||
| 2 |
(2)∵AE⊥BC,OE⊥BC,
∴BC⊥面AOE,∴面ABC⊥面AOE.
在面AOE中,作OF⊥AE,则OF⊥面ABC,
所以,OF的长即为点O到面ABC的距离.
∵△AOE是等腰三角形,DE是底AO上的高,OF是AE边上的高,
∴由面积公式得:
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
解得.OF=
| ||
| 3 |
| ||
| 3 |
点评:本题考查点、线、面间的距离计算,解题时要认真审题,注意立体几何性质的合理运用,恰当地把空间距离等价转化为平面距离进行计算.

练习册系列答案
相关题目
 如图,空间四边形OABC中,
如图,空间四边形OABC中, 已知如图,空间四边形OABC,其对角线为OB、AC,M、N分别是对边OA、BC的中点,点G在线段MN上,且使MG=2GN,
已知如图,空间四边形OABC,其对角线为OB、AC,M、N分别是对边OA、BC的中点,点G在线段MN上,且使MG=2GN, 如图,空间四边形OABC中,
如图,空间四边形OABC中,