题目内容
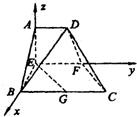
已知如图1,在梯形ABCD中,AD∥BC,∠ABC=
,AB=BC=2AD=2,E、F分别为线段AB、CD的动点,且EF∥BC,G是BC的中点,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图2).
(1)当AE为何值时,BD⊥EG;
(2)在(1)的条件下,求BD与平面ABF所成角的大小.

| π | 2 |
(1)当AE为何值时,BD⊥EG;
(2)在(1)的条件下,求BD与平面ABF所成角的大小.

分析:(1)沿EF将梯形ABCD翻折后,建立空间坐标系,设EA=t,t∈(0,2),求出
和
的坐标,由BD⊥EG,得
•
=0,解方程求得t的值.
(2)在(1)的条件下,求出
、
的坐标,设出平面ABF的法向量为
的坐标,由
•
=0,
•
=0,解得
的坐标,设BD与平面ABF所成角为θ,则由sinθ=cos<
,
>
=
,运算求得结果,即可得到θ的值.
| BD |
| EG |
| BD |
| EG |
(2)在(1)的条件下,求出
| BA |
| BF |
| n |
| n |
| BA |
| n |
| BF |
| n |
| BD |
| n |
=
| ||||
|
|
解答:解:(1)沿EF将梯形ABCD翻折后,以EF所在直线为x轴,以EB所在直线为y轴,以EA所在的直线为z轴,建立空间坐标系,设EA=t,t∈(0,2).
则A(0,0,t ),B(2-t,0,0 ),D(0,1,t),G(2-t,1,0).
∴
=(t-2,1,t),
=(2-t,1,0).
∵BD⊥EG,
∴
•
=0,即-(t-2)2+1=0,解得 t=1 或t=3(舍去).
故EA=1.
(2)在(1)的条件下,A(0,0,1 ),B( 1,0,0 ),F(0,
,0 ),D(0,1,1 ),
=(-1,1,1),
=(-1,0 1),
=(-1,
,0 ).
设平面ABF的法向量为
=(a,b,1),由
•
=0,
•
=0,解得 a=-1,b=1,故
=(-1,1,1).
设BD与平面ABF所成角为θ,则 sinθ=cos<
,
>=
=
=
,
∴θ=arcsin
. 
则A(0,0,t ),B(2-t,0,0 ),D(0,1,t),G(2-t,1,0).
∴
| BD |
| EG |
∵BD⊥EG,
∴
| BD |
| EG |
故EA=1.
(2)在(1)的条件下,A(0,0,1 ),B( 1,0,0 ),F(0,
| 3 |
| 2 |
| BD |
| BA |
| BF |
| 3 |
| 2 |
设平面ABF的法向量为
| n |
| n |
| BA |
| n |
| BF |
| n |
设BD与平面ABF所成角为θ,则 sinθ=cos<
| BD |
| n |
| ||||
|
|
|-1+
| ||||||
|
| ||
| 33 |
∴θ=arcsin
| ||
| 33 |

点评:本题主要考查直线和平面所成的角的定义和求法,两个向量坐标形式的运算,两个向量夹角公式的应用,体现了等价转化和数形结合的数学思想,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目

 (II)求证:BE⊥平面PCD;
(II)求证:BE⊥平面PCD; (II)求证:BE⊥平面PCD;
(II)求证:BE⊥平面PCD;