题目内容
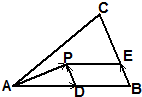 设D为△ABC的边AB的中点,P为△ABC内一点,且满足,
设D为△ABC的边AB的中点,P为△ABC内一点,且满足,| AP |
| AD |
| 2 |
| 5 |
| BC |
| S△APD |
| S△ABC |
分析:利用平面向量基本定理将
表示出来,从而可以得到四边形DPEB为平行四边形,再利用三角形面积公式,从而可求三角形的面积之比.
| AP |
解答:解:如图
=
=
∴
+
=
+
=
四边形DPEB为平行四边形,
=
=
,
故选C
| DP |
| BE |
| 2 |
| 5 |
| BC |
∴
| AD |
| 2 |
| 5 |
| BC |
| AD |
| DP |
| AP |
四边形DPEB为平行四边形,
| S△APD |
| S△ABC |
| ||
|
| 1 |
| 5 |
故选C
点评:本题的考点是向量在几何中的应用,主要考查向量的加法运算,考查三角形的面积之比,关键是由向量条件得出对应三角形的高之比.

练习册系列答案
相关题目
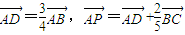 ,则
,则 =( )
=( )


