题目内容
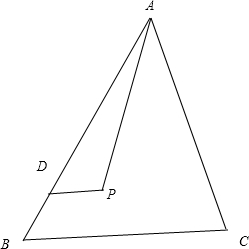
(2012•鹰潭一模)设D为△ABC的边AB上一点,P为△ABC内一点,且满足
=
,
=
+
,λ>0,则
有( )
| AD |
| λ+1 | ||
λ2+
|
| AB |
| AP |
| AD |
| λ |
| λ+1 |
| BC |
| S△APD |
| S△ABC |
分析:根据向量关系,确定DP:BC=
,△ADP的高:△ABC的高=AD:AB=
,从而可求面积之比,再利用基本不等式,即可得到结论.
| λ |
| λ+1 |
| λ+1 | ||
λ2+
|
解答:解:∵
=
+
=
+
∴
=
∴DP:BC=
∵
=
∴△ADP的高:△ABC的高=AD:AB=
∴
=
×
=
=
∵λ>0,∴λ+
≥2,当且仅当λ=1时,取等号
∴当λ=1时,
取得最大值
=
=1-
故选D.
| AP |
| AD |
| λ |
| λ+1 |
| BC |
| AD |
| DP |

∴
| DP |
| λ |
| λ+1 |
| BC |
∴DP:BC=
| λ |
| λ+1 |
∵
| AD |
| λ+1 | ||
λ2+
|
| AB |
∴△ADP的高:△ABC的高=AD:AB=
| λ+1 | ||
λ2+
|
∴
| S△APD |
| S△ABC |
| λ |
| λ+1 |
| λ+1 | ||
λ2+
|
| λ | ||
λ2+
|
| 1 | ||||
λ+
|
∵λ>0,∴λ+
| 1 |
| λ |
∴当λ=1时,
| S△APD |
| S△ABC |
| 1 | ||
2+
|
2-
| ||
| 2 |
| ||
| 2 |
故选D.
点评:本题考查向量知识的运用,考查三角形的面积,考查基本不等式的运用,解题的关键是确定面积之比.

练习册系列答案
相关题目