题目内容
正四面体P-ABC中,点M在面PBC内,且点M到点P的距离等于点M到底面ABC的距离则动点M在面PBC的轨迹是( )
分析:过M作MO⊥面ABC,垂足为O,过M作MD⊥BC,垂足为D,连接OD,则OD⊥BC,可知∠MDO为侧面PBC与底面ABC所成的二面角的平面角α,进而由点M到点P的距离等于点M到底面ABC的距离,可确定轨迹.
解答:解:由题意,过M作MO⊥面ABC,垂足为O,过M作MD⊥BC,垂足为D,连接OD,则OD⊥BC
∴∠MDO为侧面PBC与底面ABC所成的二面角的平面角α
∴OM=MDsinα
∵MP=MO
∴MP=MDsinα
∴
=sinα
∵0<sinα<1
∴轨迹是椭圆的一部分
故选B.
∴∠MDO为侧面PBC与底面ABC所成的二面角的平面角α
∴OM=MDsinα
∵MP=MO
∴MP=MDsinα
∴
| MP |
| MD |
∵0<sinα<1
∴轨迹是椭圆的一部分
故选B.
点评:本题以正四面体为载体,考查轨迹问题,关键是合理运用定义.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
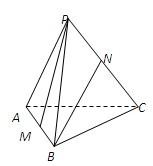 如图,已知正四面体P-ABC中,棱AB、PC的中点分别是M、N.
如图,已知正四面体P-ABC中,棱AB、PC的中点分别是M、N. 在正四面体P-ABC中,D,E,F分别是AB、BC、CA的中点,求证:
在正四面体P-ABC中,D,E,F分别是AB、BC、CA的中点,求证: