题目内容
有如下结论：“圆x
2+y
2=r
2上一点P（x
0，y
0）处的切线方程为x
0y+y
0y=r
2”，类比也有结论：“椭圆
+=1(a＞b＞0)上一点P(x0，y0)处的切线方程为
+=1”，过椭圆C：
+y2=1的右准线l上任意一点M引椭圆C的两条切线，切点为A、B．
（1）求证：直线AB恒过一定点；
（2）当点M的纵坐标为1时，求△ABM的面积．
分析：（1）设出M的坐标，及2个切点的坐标，由椭圆方程写出切线方程，把M的坐标代入切线方程，得到2个切点所在的直线方程，把右焦点坐标代入检验．
（2）把AB的方程代入椭圆方程，化为关于y的一元二次方程，求出2根之和、2根之积，用弦长公式求弦长|AB|，再求出M 到AB的距离d，计算面积．
解答：解：
（1）设M
(，t)(t∈R)，A(x1，y1)，B(x2，y2)，则MA的方程为+y1y=1∵点M在MA上∴
x1+ty1=1，同理可得
x2+ty2=1②（3分）
由①②知AB的方程为
x+ty=1，即x=(1-ty)（4分）
易知右焦点F（
，0）满足③式，（5分）
故AB恒过椭圆C的右焦点F（
，0）（6分）
（2）把AB的方程 x=
（1-y）代入椭圆化简得，7y
2-6y-1=0，
y
1+y
2=
，y
1•y
2=-
∴|AB|=
•|y
1-y
2|=
•
=
，
又M 到AB的距离d=
=
，
△ABM的面积 S=
•|AB|•d=
．
点评：本题考查直线过定点、弦长公式、及点到直线的距离公式．
练习册系列答案
相关题目
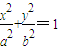，（a＞b＞0）的两焦点分别为F1、F2，
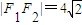，离心率
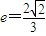．过直线l：
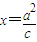上任意一点M，引椭圆C的两条切线，切点为A、B．
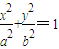（a＞b＞0），上一点P（x，y）处的切线方程”（只写类比结论，不必证明）．
）；
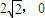，（a＞b＞0）的两焦点分别为F1、F2，
，离心率
．过直线l：
上任意一点M，引椭圆C的两条切线，切点为A、B．
（a＞b＞0），上一点P（x，y）处的切线方程”（只写类比结论，不必证明）．
）；