题目内容
已知椭圆C: ,(a>b>0)的两焦点分别为F1、F2,
,(a>b>0)的两焦点分别为F1、F2, ,离心率
,离心率 .过直线l:
.过直线l: 上任意一点M,引椭圆C的两条切线,切点为A、B.
上任意一点M,引椭圆C的两条切线,切点为A、B.(1)在圆中有如下结论:“过圆x2+y2=r2上一点P(x,y)处的切线方程为:xx+yy=r2”.由上述结论类比得到:“过椭圆
 (a>b>0),上一点P(x,y)处的切线方程”(只写类比结论,不必证明).
(a>b>0),上一点P(x,y)处的切线方程”(只写类比结论,不必证明).(2)利用(1)中的结论证明直线AB恒过定点(
 );
);(3)当点M的纵坐标为1时,求△ABM的面积.
【答案】分析:(1)由过圆上一点的切线方程,我们不难类比推断出过椭圆上一点的切线方程.
(2)由(1)的结论,我们可以设出A,B两点的坐标,列出切线方程,又由M为直线l: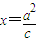 上任意一点,故可知M为两条切线与l的公共交点,消参后即得答案.
上任意一点,故可知M为两条切线与l的公共交点,消参后即得答案.
(3)由(2)中结论,我们可得M点的坐标,根据l的方程我们可以计算出AB边上的高,再由弦长公式计算出AB的长度,代入三角形面积公式即可.
解答:解:(1)类比过圆上一点的切线方程,可合情推理:
过椭圆 (a>b>0),上一点P(x,y)处的切线方程为
(a>b>0),上一点P(x,y)处的切线方程为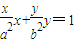 .
.
(2)由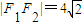 ,离心率
,离心率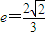
得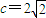 ,a=3∴b=1
,a=3∴b=1
∴椭圆C的方程为: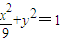
l的方程为: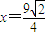
设A(x1,y1),B(x2,y2),M的纵坐标为t,即 ,
,
由(1)的结论
∴MA的方程为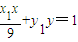
又其过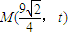 点,
点,
∴
同理有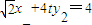
∴点A(x1,y1),B(x2,y2)在直线 上;
上;
当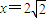 ,y=0时,方程
,y=0时,方程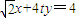 恒成立,
恒成立,
∴直线AB过定点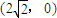
(3)t=1∴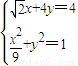 消去y得
消去y得 ,
,
∴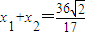 ,x1x2=0,
,x1x2=0,


∴ .
.
点评:本题综合的考查了椭圆与直线的相关知识点,本题的切入点是由类比思想探究出的过椭圆上一点的切线方程,运用设而不求的方法探究出切点A,B的坐标满足的共同性质,从而得到两切点确定的直线系的方程,并由直线系方程得到结论直线过定点;已知三角形一顶点坐标和对边所在的直线,我们可以代入点到直线距离公式求出该边上三角形的高,再由边长不难得到面积.
(2)由(1)的结论,我们可以设出A,B两点的坐标,列出切线方程,又由M为直线l:
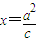 上任意一点,故可知M为两条切线与l的公共交点,消参后即得答案.
上任意一点,故可知M为两条切线与l的公共交点,消参后即得答案.(3)由(2)中结论,我们可得M点的坐标,根据l的方程我们可以计算出AB边上的高,再由弦长公式计算出AB的长度,代入三角形面积公式即可.
解答:解:(1)类比过圆上一点的切线方程,可合情推理:
过椭圆
 (a>b>0),上一点P(x,y)处的切线方程为
(a>b>0),上一点P(x,y)处的切线方程为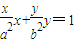 .
.(2)由
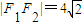 ,离心率
,离心率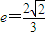
得
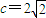 ,a=3∴b=1
,a=3∴b=1∴椭圆C的方程为:
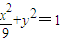
l的方程为:
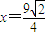
设A(x1,y1),B(x2,y2),M的纵坐标为t,即
 ,
,由(1)的结论
∴MA的方程为
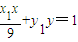
又其过
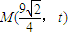 点,
点,∴

同理有
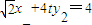
∴点A(x1,y1),B(x2,y2)在直线
 上;
上;当
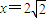 ,y=0时,方程
,y=0时,方程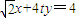 恒成立,
恒成立,∴直线AB过定点
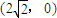
(3)t=1∴
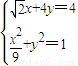 消去y得
消去y得 ,
,∴
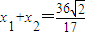 ,x1x2=0,
,x1x2=0,

∴
 .
.点评:本题综合的考查了椭圆与直线的相关知识点,本题的切入点是由类比思想探究出的过椭圆上一点的切线方程,运用设而不求的方法探究出切点A,B的坐标满足的共同性质,从而得到两切点确定的直线系的方程,并由直线系方程得到结论直线过定点;已知三角形一顶点坐标和对边所在的直线,我们可以代入点到直线距离公式求出该边上三角形的高,再由边长不难得到面积.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 已知椭圆C:
已知椭圆C: +
+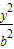 =1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )
=1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )



 +
+ =1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e.
=1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e. ,且恰好经过椭圆的右顶点,求e的大小;
,且恰好经过椭圆的右顶点,求e的大小; y+3=0相切,求椭圆方程.
y+3=0相切,求椭圆方程.
 +
+ =1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e.
=1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e. ,且恰好经过椭圆的右顶点,求e的大小;
,且恰好经过椭圆的右顶点,求e的大小; y+3=0相切,求椭圆方程.
y+3=0相切,求椭圆方程.
 +
+ =1(a>b>0)的左、右焦点分别为F
=1(a>b>0)的左、右焦点分别为F 、F
、F ,A是椭圆C上的一点,AF
,A是椭圆C上的一点,AF
 +y
+y ,y
,y =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+ =0相切。
=0相切。