题目内容
(本小题满分12分)
已知定义在R上的函数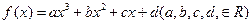 的图像关于原点对称,且x=1
的图像关于原点对称,且x=1 时,f(x)取极小值
时,f(x)取极小值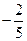 .
.
(Ⅰ)求f(x)的解析式;
(Ⅱ)当x∈[-1,1]时,图像上是否存在两点,使得在此两点处的切线互相垂直?证明你的结 论.
论.
已知定义在R上的函数
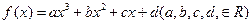 的图像关于原点对称,且x=1
的图像关于原点对称,且x=1 时,f(x)取极小值
时,f(x)取极小值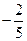 .
.(Ⅰ)求f(x)的解析式;
(Ⅱ)当x∈[-1,1]时,图像上是否存在两点,使得在此两点处的切线互相垂直?证明你的结
 论.
论.解:(Ⅰ) 因为函数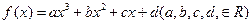 的图像关于原点对称,
的图像关于原点对称,
所以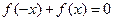 对任意
对任意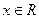 恒成立,
恒成立,
即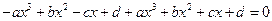 对任意
对任意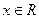 恒成立,
恒成立,
所以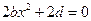 恒成立,故
恒成立,故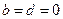 ,…………………3分
,…………………3分
故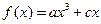 ,
,
又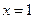 时,
时,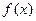 取极小值
取极小值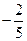 ,所以
,所以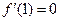 ,且
,且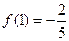 ,
,
所以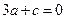 ………………①
………………①
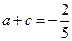 ……………………②
……………………②
解得: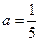 ,
,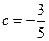 ;
;
所以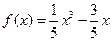 ,(
,(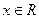 )…………………………………………………6分
)…………………………………………………6分
(Ⅱ)当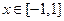 时,图像上不存在两点使得过此两点处的切线互相垂直.
时,图像上不存在两点使得过此两点处的切线互相垂直.
证明如下:(方法1,用反证法)
①假设在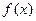 的图像上存在两点
的图像上存在两点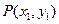 ,
,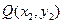 ,使得在此两点处的切线互相垂直,由(Ⅰ) 可知
,使得在此两点处的切线互相垂直,由(Ⅰ) 可知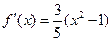 ,且在
,且在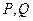 两点处的切线斜率均存在.
两点处的切线斜率均存在.
由假设 则有
则有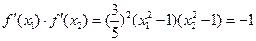 ,…………………………8分
,…………………………8分
从而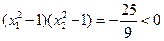 ,
,
另一方面,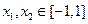 ,所以
,所以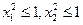 ,所以
,所以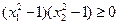 ,
,
与前式显然矛盾.所以,
当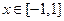 时,图像上不存在两点使得在此两点处的切线互相垂直.………………12分
时,图像上不存在两点使得在此两点处的切线互相垂直.………………12分
(方法2)
设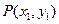 ,
,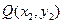 为
为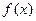 的图像上两点,由(Ⅰ) 可知
的图像上两点,由(Ⅰ) 可知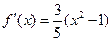 ,
,
且在点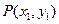 和点
和点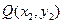 处的两条切线的斜率均存在.
处的两条切线的斜率均存在.
不妨设在点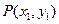 处的切线斜率为
处的切线斜率为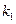 ,在点
,在点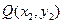 处的切线斜率为
处的切线斜率为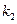 ,
,
则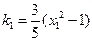 ,
,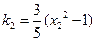 ;………………8分
;………………8分
所以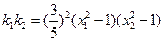 ,
,
由题意,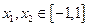 ,
,
所以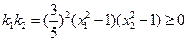 ,即
,即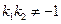
综上所述,当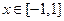 时,图像上不存在两点使得在此两点处的切线互相垂直.……12分
时,图像上不存在两点使得在此两点处的切线互相垂直.……12分
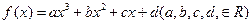 的图像关于原点对称,
的图像关于原点对称,所以
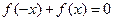 对任意
对任意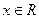 恒成立,
恒成立,即
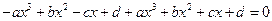 对任意
对任意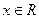 恒成立,
恒成立,所以
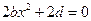 恒成立,故
恒成立,故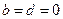 ,…………………3分
,…………………3分故
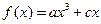 ,
,又
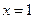 时,
时,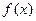 取极小值
取极小值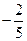 ,所以
,所以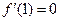 ,且
,且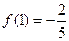 ,
,所以
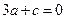 ………………①
………………①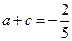 ……………………②
……………………②解得:
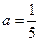 ,
,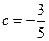 ;
;所以
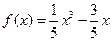 ,(
,(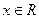 )…………………………………………………6分
)…………………………………………………6分(Ⅱ)当
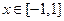 时,图像上不存在两点使得过此两点处的切线互相垂直.
时,图像上不存在两点使得过此两点处的切线互相垂直.证明如下:(方法1,用反证法)
①假设在
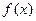 的图像上存在两点
的图像上存在两点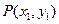 ,
,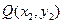 ,使得在此两点处的切线互相垂直,由(Ⅰ) 可知
,使得在此两点处的切线互相垂直,由(Ⅰ) 可知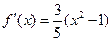 ,且在
,且在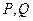 两点处的切线斜率均存在.
两点处的切线斜率均存在.由假设
 则有
则有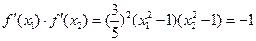 ,…………………………8分
,…………………………8分从而
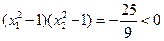 ,
,另一方面,
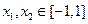 ,所以
,所以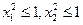 ,所以
,所以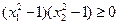 ,
,与前式显然矛盾.所以,
当
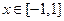 时,图像上不存在两点使得在此两点处的切线互相垂直.………………12分
时,图像上不存在两点使得在此两点处的切线互相垂直.………………12分(方法2)
设
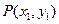 ,
,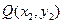 为
为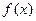 的图像上两点,由(Ⅰ) 可知
的图像上两点,由(Ⅰ) 可知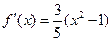 ,
,且在点
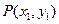 和点
和点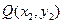 处的两条切线的斜率均存在.
处的两条切线的斜率均存在. 不妨设在点
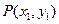 处的切线斜率为
处的切线斜率为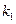 ,在点
,在点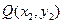 处的切线斜率为
处的切线斜率为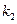 ,
,则
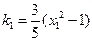 ,
,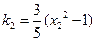 ;………………8分
;………………8分所以
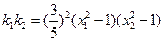 ,
,由题意,
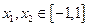 ,
,所以
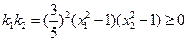 ,即
,即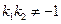
综上所述,当
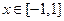 时,图像上不存在两点使得在此两点处的切线互相垂直.……12分
时,图像上不存在两点使得在此两点处的切线互相垂直.……12分略

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
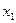 ,
,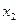 是函数
是函数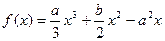 (
(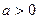 )的两个极值点,且
)的两个极值点,且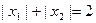 .
.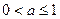 ;(2)求证:
;(2)求证: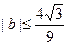 ;
;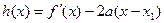 ,求证:当
,求证:当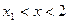 且
且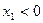 时,
时,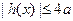 .
.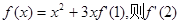 = ( )
= ( )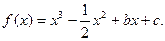 。
。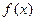 的图象有与
的图象有与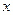 轴平行的切线,求
轴平行的切线,求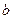 的取值范围;
的取值范围;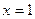 时取得极值,且
时取得极值,且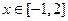 时,
时,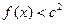 恒成立,求
恒成立,求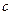 的取值范围。
的取值范围。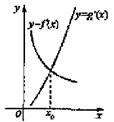
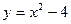 与直线y=x+2相交于A、B两点,过A、B两点的切线分别为
与直线y=x+2相交于A、B两点,过A、B两点的切线分别为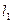 和
和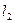 。
。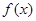 是可导函数,且
是可导函数,且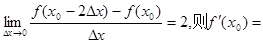 ( )
( )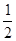
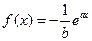 的图像在
的图像在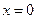 处的切线
处的切线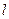 与圆
与圆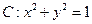 相离,则点
相离,则点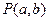 与圆
与圆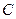 的位置关系是 .
的位置关系是 .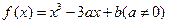 在点
在点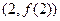 处与直线
处与直线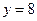 相切,则双曲线
相切,则双曲线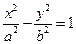 的离心率等于 .
的离心率等于 .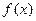 是定义在R上的奇函数,
是定义在R上的奇函数,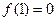 ,
,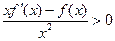
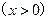 ,则不等式
,则不等式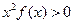 的解集是 .
的解集是 .