题目内容
设函数g(x)=x2-2(x∈R),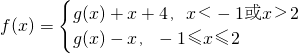 ,则f(x)的值域是
,则f(x)的值域是
- A.
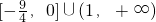
- B.[0,+∞)
- C.
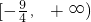
- D.
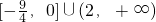
D
分析:根据x的取值范围化简f(x)的解析式,根据二次函数的性质可求每段函数的值域,再把值域取并集即可求解
解答:由题意 f(x)=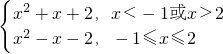
当x∈(-∞,-1)∪(2,+∞)时,由二次函数的性质可得f(x)=x2+x+2=

结合二次函数的性质可知,当x=-1时函数有最小值2
∴f(x)>2
当x∈[-1,2]时,f(x)=x2-x-2=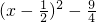
由二次函数的性质可得f(x)∈[- ,0]
,0]
综上可得[-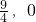 ]∪(2,+∞)
]∪(2,+∞)
故选 D
点评:本题考查分段函数值域的求法,二次函数的性质的应用,考查分类讨论的数学思想,属于基础题.
分析:根据x的取值范围化简f(x)的解析式,根据二次函数的性质可求每段函数的值域,再把值域取并集即可求解
解答:由题意 f(x)=
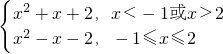
当x∈(-∞,-1)∪(2,+∞)时,由二次函数的性质可得f(x)=x2+x+2=


结合二次函数的性质可知,当x=-1时函数有最小值2
∴f(x)>2
当x∈[-1,2]时,f(x)=x2-x-2=
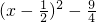
由二次函数的性质可得f(x)∈[-
 ,0]
,0]综上可得[-
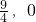 ]∪(2,+∞)
]∪(2,+∞)故选 D
点评:本题考查分段函数值域的求法,二次函数的性质的应用,考查分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目