题目内容
椭圆的两个焦点是F1(-1,0),F2(1,0),P为椭圆上一点,且F1F2是PF1与PF2的等差中项,则该椭圆方程是
+
=1
+
=1.
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
分析:由于F1F2是PF1与PF2的等差中项,可得2a=|PF1|+|PF2|=2|F1F2|=4,解得a=2,又c=1.及b2=a2-c2=3,即可得出.
解答:解:椭圆的两个焦点是F1(-1,0),F2(1,0),
∵P为椭圆上一点,F1F2是PF1与PF2的等差中项,
∴2a=PF1+PF2=2F1F2=4,a=2,c=1.
∴b2=a2-c2=3,故所求椭圆的方程为
+
=1.
答案:
+
=1
∵P为椭圆上一点,F1F2是PF1与PF2的等差中项,
∴2a=PF1+PF2=2F1F2=4,a=2,c=1.
∴b2=a2-c2=3,故所求椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
答案:
| x2 |
| 4 |
| y2 |
| 3 |
点评:熟练掌握等差中项、椭圆的定义是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
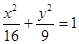 B.
B.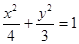
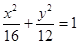 D.
D.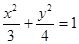
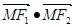 =0的点M总在椭圆的内部,则椭圆的离心率的取值范围是 ▲
=0的点M总在椭圆的内部,则椭圆的离心率的取值范围是 ▲
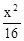 +
+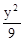 =1 B.
=1 B. 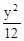 =1 C.
=1 C. 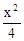 +
+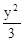 =1 D .
=1 D . 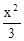 +
+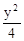 =1
=1